MINLPLib

A Library of Mixed-Integer and Continuous Nonlinear Programming Instances

Home // Instances // Documentation // Download // Statistics

Instance ann_fermentation_tanh

Fermentation process of glucose to gluconic acid learned and optimized by an embedded artificial neural network.

Formatsⓘ	ams gms mod nl osil py
Primal Bounds (infeas ≤ 1e-08)ⓘ	-99.93663292 p1 ( gdx sol ) (infeas: 3e-14)
Other points (infeas > 1e-08)ⓘ
Dual Boundsⓘ	-99.93663847 (LINDO)
Referencesⓘ	Schweidtmann, Artur M. and Mitsos, Alexander, Deterministic Global Optimization with Artificial Neural Networks Embedded, Journal of Optimization Theory and Applications, 180:3, 2019, 925-948.
Applicationⓘ	Neural Networks
Added to libraryⓘ	29 Nov 2021
Problem typeⓘ	NLP
#Variablesⓘ	12
#Binary Variablesⓘ	0
#Integer Variablesⓘ	0
#Nonlinear Variablesⓘ	4
#Nonlinear Binary Variablesⓘ	0
#Nonlinear Integer Variablesⓘ	0
Objective Senseⓘ	min
Objective typeⓘ	signomial
Objective curvatureⓘ	indefinite
#Nonzeros in Objectiveⓘ	2
#Nonlinear Nonzeros in Objectiveⓘ	2
#Constraintsⓘ	9
#Linear Constraintsⓘ	7
#Quadratic Constraintsⓘ	0
#Polynomial Constraintsⓘ	0
#Signomial Constraintsⓘ	0
#General Nonlinear Constraintsⓘ	2
Operands in Gen. Nonlin. Functionsⓘ	tanh
Constraints curvatureⓘ	indefinite
#Nonzeros in Jacobianⓘ	23
#Nonlinear Nonzeros in Jacobianⓘ	2
#Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ	5
#Nonzeros in Diagonal of Hessian of Lagrangianⓘ	3
#Blocks in Hessian of Lagrangianⓘ	3
Minimal blocksize in Hessian of Lagrangianⓘ	1
Maximal blocksize in Hessian of Lagrangianⓘ	2
Average blocksize in Hessian of Lagrangianⓘ	1.333333
#Semicontinuitiesⓘ	0
#Nonlinear Semicontinuitiesⓘ	0
#SOS type 1ⓘ	0
#SOS type 2ⓘ	0
Minimal coefficientⓘ	2.5000e-02
Maximal coefficientⓘ	1.4792e+02
Infeasibility of initial pointⓘ	101.2
Sparsity Jacobianⓘ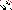
Sparsity Hessian of Lagrangianⓘ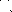

$offlisting
*
* Equation counts
*     Total        E        G        L        N        X        C        B
*        10       10        0        0        0        0        0        0
*
* Variable counts
*                  x        b        i      s1s      s2s       sc       si
*     Total     cont   binary  integer     sos1     sos2    scont     sint
*        13       13        0        0        0        0        0        0
* FX      0
*
* Nonzero counts
*     Total    const       NL
*        26       22        4

* Solve m using NLP minimizing objvar;

Variables
    objvar,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13;

Equations
    e1,e2,e3,e4,e5,e6,e7,e8,e9,e10;

e1..  91.91176470588235 * x10 / x2 + objvar =E= 0;
e2..  -tanh(x12) + x8 =E= 0;
e3..  -tanh(x13) + x9 =E= 0;
e4..  -0.0949474332688833 * x8 + 0.968637250639063 * x9 + x11 =E=
      0.002499597315649;
e5..  x10 - 86.324 * x11 =E= 92.74;
e6..  -0.025 * x2 + x5 =E= -3.5;
e7..  -x3 + x6 =E= -2;
e8..  -0.04 * x4 + x7 =E= -1.4;
e9..  -24.4380718077469 * x5 - 22.0304402344789 * x6 + 147.921509281049 * x7 +
      x12 =E= 101.235018055261;
e10..  1.48567642304727 * x5 - 0.0532843142008436 * x6 + 0.910590580134437 * x7
       + x13 =E= 0.18771256886977;

* set non-default bounds
x2.lo = 100; x2.up = 180;
x3.lo = 1; x3.up = 3;
x4.lo = 10; x4.up = 60;

Model m / all /;

m.limrow = 0;
m.tolproj=0.0;
m.limcol = 0;

$if NOT '%gams.u1%' == '' $include '%gams.u1%'

$if not set NLP $set NLP NLP
Solve m using %NLP% minimizing objvar;