MINLPLib

A Library of Mixed-Integer and Continuous Nonlinear Programming Instances

Home // Instances // Documentation // Download // Statistics

Instance batchdes

Formatsⓘ	ams gms mod nl osil py
Primal Bounds (infeas ≤ 1e-08)ⓘ	167427.6571 p1 ( gdx sol ) (infeas: 0)
Other points (infeas > 1e-08)ⓘ
Dual Boundsⓘ	167427.6563 (ALPHAECP) 167427.6571 (ANTIGONE) 167427.6571 (BARON) 167427.657 (BONMIN) 167427.6571 (COUENNE) 167427.6571 (LINDO) 167427.6571 (SCIP) 167427.6368 (SHOT)
Referencesⓘ	Kocis, Gary R and Grossmann, I E, Global Optimization of Nonconvex MINLP Problems in Process Synthesis, Industrial and Engineering Chemistry Research, 27:8, 1988, 1407-1421.
Sourceⓘ	GAMS Model Library model batchdes
Applicationⓘ	Batch processing
Added to libraryⓘ	01 May 2001
Problem typeⓘ	MBNLP
#Variablesⓘ	19
#Binary Variablesⓘ	9
#Integer Variablesⓘ	0
#Nonlinear Variablesⓘ	10
#Nonlinear Binary Variablesⓘ	0
#Nonlinear Integer Variablesⓘ	0
Objective Senseⓘ	min
Objective typeⓘ	nonlinear
Objective curvatureⓘ	convex
#Nonzeros in Objectiveⓘ	6
#Nonlinear Nonzeros in Objectiveⓘ	6
#Constraintsⓘ	19
#Linear Constraintsⓘ	18
#Quadratic Constraintsⓘ	0
#Polynomial Constraintsⓘ	0
#Signomial Constraintsⓘ	0
#General Nonlinear Constraintsⓘ	1
Operands in Gen. Nonlin. Functionsⓘ	exp
Constraints curvatureⓘ	convex
#Nonzeros in Jacobianⓘ	46
#Nonlinear Nonzeros in Jacobianⓘ	4
#Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ	20
#Nonzeros in Diagonal of Hessian of Lagrangianⓘ	10
#Blocks in Hessian of Lagrangianⓘ	5
Minimal blocksize in Hessian of Lagrangianⓘ	2
Maximal blocksize in Hessian of Lagrangianⓘ	2
Average blocksize in Hessian of Lagrangianⓘ	2.0
#Semicontinuitiesⓘ	0
#Nonlinear Semicontinuitiesⓘ	0
#SOS type 1ⓘ	0
#SOS type 2ⓘ	0
Minimal coefficientⓘ	6.0000e-01
Maximal coefficientⓘ	2.0000e+05
Infeasibility of initial pointⓘ	517.1
Sparsity Jacobianⓘ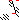
Sparsity Hessian of Lagrangianⓘ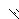

$offlisting
*  
*  Equation counts
*      Total        E        G        L        N        X        C        B
*         20        7       12        1        0        0        0        0
*  
*  Variable counts
*                   x        b        i      s1s      s2s       sc       si
*      Total     cont   binary  integer     sos1     sos2    scont     sint
*         20       11        9        0        0        0        0        0
*  FX      0
*  
*  Nonzero counts
*      Total    const       NL      DLL
*         53       43       10        0
*
*  Solve m using MINLP minimizing objvar;


Variables  b1,b2,b3,b4,b5,b6,b7,b8,b9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19
          ,objvar;

Positive Variables  x17,x18,x19;

Binary Variables  b1,b2,b3,b4,b5,b6,b7,b8,b9;

Equations  e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13,e14,e15,e16,e17,e18,e19
          ,e20;


e1..    x10 - x13 =G= 0.693147180559945;

e2..    x11 - x13 =G= 1.09861228866811;

e3..    x12 - x13 =G= 1.38629436111989;

e4..    x10 - x14 =G= 1.38629436111989;

e5..    x11 - x14 =G= 1.79175946922805;

e6..    x12 - x14 =G= 1.09861228866811;

e7..    x15 + x17 =G= 2.07944154167984;

e8..    x15 + x18 =G= 2.99573227355399;

e9..    x15 + x19 =G= 1.38629436111989;

e10..    x16 + x17 =G= 2.30258509299405;

e11..    x16 + x18 =G= 2.484906649788;

e12..    x16 + x19 =G= 1.09861228866811;

e13.. 200000*exp(x15 - x13) + 150000*exp(x16 - x14) =L= 6000;

e14..  - 0.693147180559945*b4 - 1.09861228866811*b7 + x17 =E= 0;

e15..  - 0.693147180559945*b5 - 1.09861228866811*b8 + x18 =E= 0;

e16..  - 0.693147180559945*b6 - 1.09861228866811*b9 + x19 =E= 0;

e17..    b1 + b4 + b7 =E= 1;

e18..    b2 + b5 + b8 =E= 1;

e19..    b3 + b6 + b9 =E= 1;

e20.. -(250*exp(0.6*x10 + x17) + 500*exp(0.6*x11 + x18) + 340*exp(0.6*x12 + x19
      )) + objvar =E= 0;

* set non-default bounds
x10.lo = 5.52146091786225; x10.up = 7.82404601085629;
x11.lo = 5.52146091786225; x11.up = 7.82404601085629;
x12.lo = 5.52146091786225; x12.up = 7.82404601085629;
x13.lo = 5.40367788220586; x13.up = 6.4377516497364;
x14.lo = 4.60517018598809; x14.up = 6.03228654162824;
x15.lo = 1.89711998488588; x15.up = 2.99573227355399;
x16.lo = 1.38629436111989; x16.up = 2.484906649788;
x17.up = 1.09861228866811;
x18.up = 1.09861228866811;
x19.up = 1.09861228866811;

* set non-default levels
x10.l = 6.70502272492805;
x11.l = 7.11048783303622;
x12.l = 7.30700912709102;
x13.l = 5.92071476597113;
x14.l = 5.31872836380816;

Model m / all /;

m.limrow=0; m.limcol=0;
m.tolproj=0.0;

$if NOT '%gams.u1%' == '' $include '%gams.u1%'

$if not set MINLP $set MINLP MINLP
Solve m using %MINLP% minimizing objvar;