MINLPLib
A Library of Mixed-Integer and Continuous Nonlinear Programming Instances
Home // Instances // Documentation // Download // Statistics
Instance ex8_4_3
| Formatsⓘ | ams gms mod nl osil py |
| Primal Bounds (infeas ≤ 1e-08)ⓘ | |
| Other points (infeas > 1e-08)ⓘ | |
| Dual Boundsⓘ | 0.00464606 (ANTIGONE) 0.00464962 (BARON) 0.00464972 (COUENNE) 0.00464972 (LINDO) 0.00464781 (SCIP) |
| Referencesⓘ | Floudas, C A, Pardalos, Panos M, Adjiman, C S, Esposito, W R, Gumus, Zeynep H, Harding, S T, Klepeis, John L, Meyer, Clifford A, and Schweiger, C A, Handbook of Test Problems in Local and Global Optimization, Kluwer Academic Publishers, 1999. Esposito, W R and Floudas, C A, Global Optimization in Parameter Estimation of Nonlinear Algebraic Models via the Error-in-Variables Approach, Industrial and Engineering Chemistry Research, 37:5, 1998, 1841-1858. Tjoa, I B and Biegler, L T, Reduced Successive Quadratic Programming Strategy for Errors-in-Variables Estimation, Computers and Chemical Engineering, 16:6, 1992, 523-533. Rod, V and Hancil, V, Iterative Estimation of Model Parameters When Measurements of All Variables are Subject to Error, Computers and Chemical Engineering, 4:2, 1980, 33-38. |
| Sourceⓘ | Test Problem ex8.4.3 of Chapter 8 of Floudas e.a. handbook |
| Added to libraryⓘ | 31 Jul 2001 |
| Problem typeⓘ | NLP |
| #Variablesⓘ | 52 |
| #Binary Variablesⓘ | 0 |
| #Integer Variablesⓘ | 0 |
| #Nonlinear Variablesⓘ | 51 |
| #Nonlinear Binary Variablesⓘ | 0 |
| #Nonlinear Integer Variablesⓘ | 0 |
| Objective Senseⓘ | min |
| Objective typeⓘ | quadratic |
| Objective curvatureⓘ | convex |
| #Nonzeros in Objectiveⓘ | 50 |
| #Nonlinear Nonzeros in Objectiveⓘ | 50 |
| #Constraintsⓘ | 25 |
| #Linear Constraintsⓘ | 0 |
| #Quadratic Constraintsⓘ | 0 |
| #Polynomial Constraintsⓘ | 0 |
| #Signomial Constraintsⓘ | 0 |
| #General Nonlinear Constraintsⓘ | 25 |
| Operands in Gen. Nonlin. Functionsⓘ | div |
| Constraints curvatureⓘ | indefinite |
| #Nonzeros in Jacobianⓘ | 100 |
| #Nonlinear Nonzeros in Jacobianⓘ | 50 |
| #Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ | 101 |
| #Nonzeros in Diagonal of Hessian of Lagrangianⓘ | 51 |
| #Blocks in Hessian of Lagrangianⓘ | 26 |
| Minimal blocksize in Hessian of Lagrangianⓘ | 1 |
| Maximal blocksize in Hessian of Lagrangianⓘ | 26 |
| Average blocksize in Hessian of Lagrangianⓘ | 1.961538 |
| #Semicontinuitiesⓘ | 0 |
| #Nonlinear Semicontinuitiesⓘ | 0 |
| #SOS type 1ⓘ | 0 |
| #SOS type 2ⓘ | 0 |
| Minimal coefficientⓘ | 1.1300e-01 |
| Maximal coefficientⓘ | 1.8540e+00 |
| Infeasibility of initial pointⓘ | 5.447 |
| Sparsity Jacobianⓘ |  |
| Sparsity Hessian of Lagrangianⓘ | 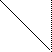 |
$offlisting
*
* Equation counts
* Total E G L N X C B
* 26 26 0 0 0 0 0 0
*
* Variable counts
* x b i s1s s2s sc si
* Total cont binary integer sos1 sos2 scont sint
* 53 53 0 0 0 0 0 0
* FX 0
*
* Nonzero counts
* Total const NL DLL
* 151 51 100 0
*
* Solve m using NLP minimizing objvar;
Variables x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19
,x20,x21,x22,x23,x24,x25,x26,x27,x28,x29,x30,x31,x32,x33,x34,x35,x36
,x37,x38,x39,x40,x41,x42,x43,x44,x45,x46,x47,x48,x49,x50,x51,x52
,objvar;
Equations e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13,e14,e15,e16,e17,e18,e19
,e20,e21,e22,e23,e24,e25,e26;
e1.. -(sqr((-0.113) + x1) + sqr((-1.851) + x2) + sqr((-0.126) + x3) + sqr((-
1.854) + x4) + sqr((-0.172) + x5) + sqr((-1.849) + x6) + sqr((-0.155) + x7
) + sqr((-1.815) + x8) + sqr((-0.219) + x9) + sqr((-1.828) + x10) + sqr((-
0.245) + x11) + sqr((-1.847) + x12) + sqr((-0.274) + x13) + sqr((-1.804)
+ x14) + sqr((-0.264) + x15) + sqr((-1.832) + x16) + sqr((-0.312) + x17)
+ sqr((-1.838) + x18) + sqr((-0.324) + x19) + sqr((-1.817) + x20) + sqr((
-0.333) + x21) + sqr((-1.82) + x22) + sqr((-0.399) + x23) + sqr((-1.845)
+ x24) + sqr((-0.417) + x25) + sqr((-1.829) + x26) + sqr((-0.419) + x27)
+ sqr((-1.832) + x28) + sqr((-0.439) + x29) + sqr((-1.82) + x30) + sqr((-
0.475) + x31) + sqr((-1.82) + x32) + sqr((-0.506) + x33) + sqr((-1.799) +
x34) + sqr((-0.538) + x35) + sqr((-1.838) + x36) + sqr((-0.538) + x37) +
sqr((-1.835) + x38) + sqr((-0.591) + x39) + sqr((-1.811) + x40) + sqr((-
0.578) + x41) + sqr((-1.794) + x42) + sqr((-0.626) + x43) + sqr((-1.825)
+ x44) + sqr((-0.659) + x45) + sqr((-1.801) + x46) + sqr((-0.668) + x47)
+ sqr((-1.81) + x48) + sqr((-0.687) + x49) + sqr((-1.802) + x50))
+ objvar =E= 0;
e2.. 1/(x1 - x52) - x2 + x51 =E= 0;
e3.. 1/(x3 - x52) - x4 + x51 =E= 0;
e4.. 1/(x5 - x52) - x6 + x51 =E= 0;
e5.. 1/(x7 - x52) - x8 + x51 =E= 0;
e6.. 1/(x9 - x52) - x10 + x51 =E= 0;
e7.. 1/(x11 - x52) - x12 + x51 =E= 0;
e8.. 1/(x13 - x52) - x14 + x51 =E= 0;
e9.. 1/(x15 - x52) - x16 + x51 =E= 0;
e10.. 1/(x17 - x52) - x18 + x51 =E= 0;
e11.. 1/(x19 - x52) - x20 + x51 =E= 0;
e12.. 1/(x21 - x52) - x22 + x51 =E= 0;
e13.. 1/(x23 - x52) - x24 + x51 =E= 0;
e14.. 1/(x25 - x52) - x26 + x51 =E= 0;
e15.. 1/(x27 - x52) - x28 + x51 =E= 0;
e16.. 1/(x29 - x52) - x30 + x51 =E= 0;
e17.. 1/(x31 - x52) - x32 + x51 =E= 0;
e18.. 1/(x33 - x52) - x34 + x51 =E= 0;
e19.. 1/(x35 - x52) - x36 + x51 =E= 0;
e20.. 1/(x37 - x52) - x38 + x51 =E= 0;
e21.. 1/(x39 - x52) - x40 + x51 =E= 0;
e22.. 1/(x41 - x52) - x42 + x51 =E= 0;
e23.. 1/(x43 - x52) - x44 + x51 =E= 0;
e24.. 1/(x45 - x52) - x46 + x51 =E= 0;
e25.. 1/(x47 - x52) - x48 + x51 =E= 0;
e26.. 1/(x49 - x52) - x50 + x51 =E= 0;
* set non-default bounds
x1.lo = -0.387; x1.up = 0.613;
x2.lo = 1.351; x2.up = 2.351;
x3.lo = -0.374; x3.up = 0.626;
x4.lo = 1.354; x4.up = 2.354;
x5.lo = -0.328; x5.up = 0.672;
x6.lo = 1.349; x6.up = 2.349;
x7.lo = -0.345; x7.up = 0.655;
x8.lo = 1.315; x8.up = 2.315;
x9.lo = -0.281; x9.up = 0.719;
x10.lo = 1.328; x10.up = 2.328;
x11.lo = -0.255; x11.up = 0.745;
x12.lo = 1.347; x12.up = 2.347;
x13.lo = -0.226; x13.up = 0.774;
x14.lo = 1.304; x14.up = 2.304;
x15.lo = -0.236; x15.up = 0.764;
x16.lo = 1.332; x16.up = 2.332;
x17.lo = -0.188; x17.up = 0.812;
x18.lo = 1.338; x18.up = 2.338;
x19.lo = -0.176; x19.up = 0.824;
x20.lo = 1.317; x20.up = 2.317;
x21.lo = -0.167; x21.up = 0.833;
x22.lo = 1.32; x22.up = 2.32;
x23.lo = -0.101; x23.up = 0.899;
x24.lo = 1.345; x24.up = 2.345;
x25.lo = -0.083; x25.up = 0.917;
x26.lo = 1.329; x26.up = 2.329;
x27.lo = -0.081; x27.up = 0.919;
x28.lo = 1.332; x28.up = 2.332;
x29.lo = -0.061; x29.up = 0.939;
x30.lo = 1.32; x30.up = 2.32;
x31.lo = -0.025; x31.up = 0.975;
x32.lo = 1.32; x32.up = 2.32;
x33.lo = 0.00600000000000001; x33.up = 1.006;
x34.lo = 1.299; x34.up = 2.299;
x35.lo = 0.038; x35.up = 1.038;
x36.lo = 1.338; x36.up = 2.338;
x37.lo = 0.038; x37.up = 1.038;
x38.lo = 1.335; x38.up = 2.335;
x39.lo = 0.091; x39.up = 1.091;
x40.lo = 1.311; x40.up = 2.311;
x41.lo = 0.078; x41.up = 1.078;
x42.lo = 1.294; x42.up = 2.294;
x43.lo = 0.126; x43.up = 1.126;
x44.lo = 1.325; x44.up = 2.325;
x45.lo = 0.159; x45.up = 1.159;
x46.lo = 1.301; x46.up = 2.301;
x47.lo = 0.168; x47.up = 1.168;
x48.lo = 1.31; x48.up = 2.31;
x49.lo = 0.187; x49.up = 1.187;
x50.lo = 1.302; x50.up = 2.302;
x51.lo = 1; x51.up = 10;
x52.lo = 2; x52.up = 10;
* set non-default levels
x1.l = -0.215252868;
x2.l = 2.194266708;
x3.l = 0.176375356;
x4.l = 1.655137904;
x5.l = -0.035787883;
x6.l = 1.573052867;
x7.l = 0.00483050400000007;
x8.l = 2.171270347;
x9.l = -0.213886277;
x10.l = 1.828210669;
x11.l = 0.743117627;
x12.l = 1.925733378;
x13.l = 0.765133039;
x14.l = 2.066250467;
x15.l = -0.105307517;
x16.l = 1.971718759;
x17.l = -0.028482136;
x18.l = 1.588080533;
x19.l = 0.492928609;
x20.l = 1.752356381;
x21.l = 0.192700266;
x22.l = 1.671441368;
x23.l = 0.03049159;
x24.l = 1.495101788;
x25.l = 0.50611365;
x26.l = 2.159892812;
x27.l = 0.149815738;
x28.l = 1.99773446;
x29.l = 0.714857606;
x30.l = 1.623658477;
x31.l = 0.085492291;
x32.l = 1.822384866;
x33.l = 0.166172762;
x34.l = 2.171462311;
x35.l = 0.303114545;
x36.l = 1.623814322;
x37.l = 0.631955922;
x38.l = 2.057719071;
x39.l = 0.719248677;
x40.l = 1.774797865;
x41.l = 0.491306994;
x42.l = 1.411695357;
x43.l = 0.440212267;
x44.l = 1.371551514;
x45.l = 0.497550272;
x46.l = 1.483099593;
x47.l = 0.813727127;
x48.l = 1.870745547;
x49.l = 0.95696172;
x50.l = 1.599805864;
x51.l = 6.949956349;
x52.l = 8.046573392;
Model m / all /;
m.limrow=0; m.limcol=0;
m.tolproj=0.0;
$if NOT '%gams.u1%' == '' $include '%gams.u1%'
$if not set NLP $set NLP NLP
Solve m using %NLP% minimizing objvar;
Last updated: 2025-08-07 Git hash: e62cedfc