MINLPLib

A Library of Mixed-Integer and Continuous Nonlinear Programming Instances

Home // Instances // Documentation // Download // Statistics

Instance ex8_4_4

Formatsⓘ	ams gms mod nl osil py
Primal Bounds (infeas ≤ 1e-08)ⓘ	0.21245984 p1 ( gdx sol ) (infeas: 3e-10)
Other points (infeas > 1e-08)ⓘ
Dual Boundsⓘ	0.21245744 (ANTIGONE) 0.21245932 (BARON) 0.21245984 (COUENNE) 0.21245901 (LINDO) 0.21245774 (SCIP)
Referencesⓘ	Floudas, C A, Pardalos, Panos M, Adjiman, C S, Esposito, W R, Gumus, Zeynep H, Harding, S T, Klepeis, John L, Meyer, Clifford A, and Schweiger, C A, Handbook of Test Problems in Local and Global Optimization, Kluwer Academic Publishers, 1999. Esposito, W R and Floudas, C A, Global Optimization in Parameter Estimation of Nonlinear Algebraic Models via the Error-in-Variables Approach, Industrial and Engineering Chemistry Research, 37:5, 1998, 1841-1858. Csendes, T and Ratz, D, Subdivision Direction Selection in Interval Methods for Global Optimization, SIAM Journal on Numerical Analysis, 34:3, 1997, 922-938.
Sourceⓘ	Test Problem ex8.4.4 of Chapter 8 of Floudas e.a. handbook
Added to libraryⓘ	31 Jul 2001
Problem typeⓘ	NLP
#Variablesⓘ	17
#Binary Variablesⓘ	0
#Integer Variablesⓘ	0
#Nonlinear Variablesⓘ	15
#Nonlinear Binary Variablesⓘ	0
#Nonlinear Integer Variablesⓘ	0
Objective Senseⓘ	min
Objective typeⓘ	quadratic
Objective curvatureⓘ	convex
#Nonzeros in Objectiveⓘ	12
#Nonlinear Nonzeros in Objectiveⓘ	12
#Constraintsⓘ	12
#Linear Constraintsⓘ	0
#Quadratic Constraintsⓘ	0
#Polynomial Constraintsⓘ	0
#Signomial Constraintsⓘ	0
#General Nonlinear Constraintsⓘ	12
Operands in Gen. Nonlin. Functionsⓘ	cvpower div
Constraints curvatureⓘ	indefinite
#Nonzeros in Jacobianⓘ	48
#Nonlinear Nonzeros in Jacobianⓘ	24
#Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ	17
#Nonzeros in Diagonal of Hessian of Lagrangianⓘ	13
#Blocks in Hessian of Lagrangianⓘ	13
Minimal blocksize in Hessian of Lagrangianⓘ	1
Maximal blocksize in Hessian of Lagrangianⓘ	3
Average blocksize in Hessian of Lagrangianⓘ	1.153846
#Semicontinuitiesⓘ	0
#Nonlinear Semicontinuitiesⓘ	0
#SOS type 1ⓘ	0
#SOS type 2ⓘ	0
Minimal coefficientⓘ	1.0000e-01
Maximal coefficientⓘ	5.0000e+00
Infeasibility of initial pointⓘ	3.131
Sparsity Jacobianⓘ
Sparsity Hessian of Lagrangianⓘ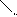

$offlisting
*  
*  Equation counts
*      Total        E        G        L        N        X        C        B
*         13       13        0        0        0        0        0        0
*  
*  Variable counts
*                   x        b        i      s1s      s2s       sc       si
*      Total     cont   binary  integer     sos1     sos2    scont     sint
*         18       18        0        0        0        0        0        0
*  FX      0
*  
*  Nonzero counts
*      Total    const       NL      DLL
*         61       25       36        0
*
*  Solve m using NLP minimizing objvar;


Variables  x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,objvar;

Negative Variables  x6;

Positive Variables  x13,x14,x16,x17;

Equations  e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13;


e1.. -(sqr((-5) + x1) + sqr(5 + x2) + sqr((-3) + x3) + sqr(2 + x4) + sqr((-2)
      + x5) + sqr(1 + x6) + sqr((-1.5) + x7) + sqr(0.5 + x8) + sqr((-1.2) + x9)
      + sqr(0.2 + x10) + sqr((-1.1) + x11) + sqr(0.1 + x12)) + objvar =E= 0;

e2.. x14/0.1570795**x15 - x1 + x13 =E= 0;

e3.. x14/0.314159**x15 - x3 + x13 =E= 0;

e4.. x14/0.4712385**x15 - x5 + x13 =E= 0;

e5.. x14/0.628318**x15 - x7 + x13 =E= 0;

e6.. x14/0.7853975**x15 - x9 + x13 =E= 0;

e7.. x14/0.942477**x15 - x11 + x13 =E= 0;

e8.. -x17/0.1570795**x15 - x2 + 0.1570795*x16 =E= 0;

e9.. -x17/0.314159**x15 - x4 + 0.314159*x16 =E= 0;

e10.. -x17/0.4712385**x15 - x6 + 0.4712385*x16 =E= 0;

e11.. -x17/0.628318**x15 - x8 + 0.628318*x16 =E= 0;

e12.. -x17/0.7853975**x15 - x10 + 0.7853975*x16 =E= 0;

e13.. -x17/0.942477**x15 - x12 + 0.942477*x16 =E= 0;

* set non-default bounds
x1.lo = 4; x1.up = 6;
x2.lo = -6; x2.up = -4;
x3.lo = 2; x3.up = 4;
x4.lo = -3; x4.up = -1;
x5.lo = 1; x5.up = 3;
x6.lo = -2;
x7.lo = 0.5; x7.up = 2.5;
x8.lo = -1.5; x8.up = 0.5;
x9.lo = 0.2; x9.up = 2.2;
x10.lo = -1.2; x10.up = 0.8;
x11.lo = 0.1; x11.up = 2.1;
x12.lo = -1.1; x12.up = 0.9;
x13.up = 1;
x14.up = 1;
x15.lo = 1.1; x15.up = 1.3;
x16.up = 1;
x17.up = 1;

* set non-default levels
x1.l = 4.343494264;
x2.l = -4.313466584;
x3.l = 3.100750712;
x4.l = -2.397724192;
x5.l = 1.584424234;
x6.l = -1.551894266;
x7.l = 1.199661008;
x8.l = 0.212540694;
x9.l = 0.334227446;
x10.l = -0.199578662;
x11.l = 2.096235254;
x12.l = 0.057466756;
x13.l = 0.991133039;
x14.l = 0.762250467;
x15.l = 1.1261384966;
x16.l = 0.639718759;
x17.l = 0.159517864;

Model m / all /;

m.limrow=0; m.limcol=0;
m.tolproj=0.0;

$if NOT '%gams.u1%' == '' $include '%gams.u1%'

$if not set NLP $set NLP NLP
Solve m using %NLP% minimizing objvar;