MINLPLib
A Library of Mixed-Integer and Continuous Nonlinear Programming Instances
Home // Instances // Documentation // Download // Statistics
Instance ghg_2veh
| Formatsⓘ | ams gms mod nl osil py |
| Primal Bounds (infeas ≤ 1e-08)ⓘ | |
| Other points (infeas > 1e-08)ⓘ | |
| Dual Boundsⓘ | 0.00000000 (ANTIGONE) 7.38244793 (BARON) 6.24967114 (COUENNE) 7.21101345 (GUROBI) 7.09617548 (LINDO) 7.43354565 (SCIP) 0.00000000 (SHOT) 7.19068586 (XPRESS) |
| Referencesⓘ | Shiau, Ching-Shin N and Michalek, Jeremy J, Global Optimization of Plug-In Hybrid Vehicle Design and Allocation to Minimize Life Cycle Greenhouse Gas Emissions, ASME Journal of Mechanical Design, 133:8, 2011, 084502. |
| Applicationⓘ | Optimal vehicle allocation for minimizing greenhouse gas emissions |
| Added to libraryⓘ | 29 Aug 2011 |
| Problem typeⓘ | MBNLP |
| #Variablesⓘ | 57 |
| #Binary Variablesⓘ | 18 |
| #Integer Variablesⓘ | 0 |
| #Nonlinear Variablesⓘ | 49 |
| #Nonlinear Binary Variablesⓘ | 18 |
| #Nonlinear Integer Variablesⓘ | 0 |
| Objective Senseⓘ | min |
| Objective typeⓘ | linear |
| Objective curvatureⓘ | linear |
| #Nonzeros in Objectiveⓘ | 2 |
| #Nonlinear Nonzeros in Objectiveⓘ | 0 |
| #Constraintsⓘ | 62 |
| #Linear Constraintsⓘ | 14 |
| #Quadratic Constraintsⓘ | 24 |
| #Polynomial Constraintsⓘ | 10 |
| #Signomial Constraintsⓘ | 2 |
| #General Nonlinear Constraintsⓘ | 12 |
| Operands in Gen. Nonlin. Functionsⓘ | div exp mul |
| Constraints curvatureⓘ | indefinite |
| #Nonzeros in Jacobianⓘ | 212 |
| #Nonlinear Nonzeros in Jacobianⓘ | 154 |
| #Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ | 493 |
| #Nonzeros in Diagonal of Hessian of Lagrangianⓘ | 17 |
| #Blocks in Hessian of Lagrangianⓘ | 1 |
| Minimal blocksize in Hessian of Lagrangianⓘ | 49 |
| Maximal blocksize in Hessian of Lagrangianⓘ | 49 |
| Average blocksize in Hessian of Lagrangianⓘ | 49.0 |
| #Semicontinuitiesⓘ | 0 |
| #Nonlinear Semicontinuitiesⓘ | 0 |
| #SOS type 1ⓘ | 0 |
| #SOS type 2ⓘ | 0 |
| Minimal coefficientⓘ | 9.4030e-05 |
| Maximal coefficientⓘ | 5.1870e+03 |
| Infeasibility of initial pointⓘ | 52.6 |
| Sparsity Jacobianⓘ |  |
| Sparsity Hessian of Lagrangianⓘ | 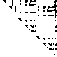 |
$offlisting
*
* Equation counts
* Total E G L N X C B
* 63 37 12 14 0 0 0 0
*
* Variable counts
* x b i s1s s2s sc si
* Total cont binary integer sos1 sos2 scont sint
* 58 40 18 0 0 0 0 0
* FX 0
*
* Nonzero counts
* Total const NL DLL
* 215 61 154 0
*
* Solve m using MINLP minimizing objvar;
Variables b1,b2,b3,b4,b5,b6,b7,b8,b9,b10,b11,b12,b13,b14,b15,b16,b17,b18,x19
,x20,x21,x22,x23,x24,x25,x26,x27,x28,x29,x30,x31,x32,x33,x34,x35,x36
,x37,x38,x39,x40,x41,x42,x43,x44,x45,x46,x47,x48,x49,x50,x51,x52,x53
,x54,x55,x56,x57,objvar;
Positive Variables x22,x26,x29,x30,x33,x34,x35,x36,x40,x44,x47,x48,x51,x52
,x53,x54,x55,x56,x57;
Binary Variables b1,b2,b3,b4,b5,b6,b7,b8,b9,b10,b11,b12,b13,b14,b15,b16,b17
,b18;
Equations e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13,e14,e15,e16,e17,e18,e19
,e20,e21,e22,e23,e24,e25,e26,e27,e28,e29,e30,e31,e32,e33,e34,e35,e36
,e37,e38,e39,e40,e41,e42,e43,e44,e45,e46,e47,e48,e49,e50,e51,e52,e53
,e54,e55,e56,e57,e58,e59,e60,e61,e62,e63;
e1.. -21.6*x21*x22*x27 + x26 =E= 0;
e2.. -(0.007852585706*x19**3 + 0.154288922601*x20**3 + 0.352933730854*x21**3 -
0.004816150342*x19**2*x20 - 0.00547943134*x20**2*x19 - 0.02533808214*x19**
2*x21 + 0.00021201136*x21**2*x19 - 0.057118497613*x20**2*x21 -
0.042739509965*x21**2*x20 - 0.01583097252*x19*x20*x21 - 0.001028174658*x19
**2 - 0.805369774847*x20**2 - 0.655580550098*x21**2 + 0.057270405947*x19*
x20 + 0.07973036236*x19*x21 + 0.342091579946*x20*x21 - 0.191345333621*x19
+ 1.188971392024*x20 - 0.346682012779*x21) + x27 =E= 4.960068215723;
e3.. -(2.21406746341*x19**3 + 1.086659693552*x20**3 + 5.577874978662*x21**3 -
0.815241697738*x19**2*x20 + 0.509578110533*x20**2*x19 + 1.561758113326*x19
**2*x21 + 2.212321055022*x21**2*x19 - 0.612567680918*x20**2*x21 +
0.254008083604*x21**2*x20 - 0.159429747244*x19*x20*x21 - 8.905599398536*
x19**2 - 6.095001164559*x20**2 - 15.207539664993*x21**2 + 0.089172114876*
x19*x20 - 3.273526677614*x19*x21 + 2.498376358946*x20*x21 + 2.621894664006
*x19 + 9.284846067558*x20 + 5.837143728557*x21) + x28 =E= 57.679680208231;
e4.. -(1.456640469666*x19**3 - 5.495718264905*x20**3 - 28.456261951645*x21**3
+ 0.912917970314*x19**2*x20 - 0.88119920631*x20**2*x19 - 1.049763024383*
x19**2*x21 - 0.308107344863*x21**2*x19 + 2.043536297441*x20**2*x21 +
15.609611231641*x21**2*x20 + 0.336486837518*x19*x20*x21 - 4.634160849469*
x19**2 + 31.478262635483*x20**2 + 34.016843490037*x21**2 + 1.153148892739*
x19*x20 + 1.168601192983*x19*x21 - 32.056936006397*x20*x21 +
3.405095041238*x19 - 54.472915571467*x20 + 9.56987912824*x21) + x23
=E= 44.230616625681;
e5.. -(3.334445194766*x19**3 - 2.265666208775*x20**3 - 20.256566414583*x21**3
+ 0.413782262402*x19**2*x20 - 3.523622273943*x20**2*x19 - 0.285910055687*
x19**2*x21 - 10.110726634622*x21**2*x19 + 1.95072196814*x20**2*x21 +
10.308512463418*x21**2*x20 + 5.808426325827*x19*x20*x21 - 6.932398033967*
x19**2 + 15.80019426934*x20**2 + 39.197963873266*x21**2 + 7.900706395772*
x19*x20 + 6.58186092156*x19*x21 - 30.119438887106*x20*x21 - 6.733798415788
*x19 - 26.385308892431*x20 - 4.098268423019*x21) + x24 =E= 32.102172356117
;
e6.. -(-0.194075741585*x19**2 - 0.004843420334*x20**2 + 0.04736686635*x21**2 +
9.4029979e-5*x19*x20 + 0.011329651793*x19*x21 - 0.001017352942*x20*x21 +
0.382275988592*x19 + 0.019484588535*x20 - 0.077357069039*x21) + x25
=E= 0.140278656706;
e7.. x23 =L= 11;
e8.. x24 =L= 11;
e9.. x25 =G= 0.32;
e10.. -21.6*x39*x40*x45 + x44 =E= 0;
e11.. -(0.007852585706*x37**3 + 0.154288922601*x38**3 + 0.352933730854*x39**3
- 0.004816150342*x37**2*x38 - 0.00547943134*x38**2*x37 - 0.02533808214*
x37**2*x39 + 0.00021201136*x39**2*x37 - 0.057118497613*x38**2*x39 -
0.042739509965*x39**2*x38 - 0.01583097252*x37*x38*x39 - 0.001028174658*
x37**2 - 0.805369774847*x38**2 - 0.655580550098*x39**2 + 0.057270405947*
x37*x38 + 0.07973036236*x37*x39 + 0.342091579946*x38*x39 - 0.191345333621
*x37 + 1.188971392024*x38 - 0.346682012779*x39) + x45 =E= 4.960068215723;
e12.. -(2.21406746341*x37**3 + 1.086659693552*x38**3 + 5.577874978662*x39**3 -
0.815241697738*x37**2*x38 + 0.509578110533*x38**2*x37 + 1.561758113326*
x37**2*x39 + 2.212321055022*x39**2*x37 - 0.612567680918*x38**2*x39 +
0.254008083604*x39**2*x38 - 0.159429747244*x37*x38*x39 - 8.905599398536*
x37**2 - 6.095001164559*x38**2 - 15.207539664993*x39**2 + 0.089172114876*
x37*x38 - 3.273526677614*x37*x39 + 2.498376358946*x38*x39 +
2.621894664006*x37 + 9.284846067558*x38 + 5.837143728557*x39) + x46
=E= 57.679680208231;
e13.. -(1.456640469666*x37**3 - 5.495718264905*x38**3 - 28.456261951645*x39**3
+ 0.912917970314*x37**2*x38 - 0.88119920631*x38**2*x37 - 1.049763024383*
x37**2*x39 - 0.308107344863*x39**2*x37 + 2.043536297441*x38**2*x39 +
15.609611231641*x39**2*x38 + 0.336486837518*x37*x38*x39 - 4.634160849469*
x37**2 + 31.478262635483*x38**2 + 34.016843490037*x39**2 + 1.153148892739
*x37*x38 + 1.168601192983*x37*x39 - 32.056936006397*x38*x39 +
3.405095041238*x37 - 54.472915571467*x38 + 9.56987912824*x39) + x41
=E= 44.230616625681;
e14.. -(3.334445194766*x37**3 - 2.265666208775*x38**3 - 20.256566414583*x39**3
+ 0.413782262402*x37**2*x38 - 3.523622273943*x38**2*x37 - 0.285910055687
*x37**2*x39 - 10.110726634622*x39**2*x37 + 1.95072196814*x38**2*x39 +
10.308512463418*x39**2*x38 + 5.808426325827*x37*x38*x39 - 6.932398033967*
x37**2 + 15.80019426934*x38**2 + 39.197963873266*x39**2 + 7.900706395772*
x37*x38 + 6.58186092156*x37*x39 - 30.119438887106*x38*x39 -
6.733798415788*x37 - 26.385308892431*x38 - 4.098268423019*x39) + x42
=E= 32.102172356117;
e15.. -(-0.194075741585*x37**2 - 0.004843420334*x38**2 + 0.04736686635*x39**2
+ 9.4029979e-5*x37*x38 + 0.011329651793*x37*x39 - 0.001017352942*x38*x39
+ 0.382275988592*x37 + 0.019484588535*x38 - 0.077357069039*x39) + x43
=E= 0.140278656706;
e16.. x41 =L= 11;
e17.. x42 =L= 11;
e18.. x43 =G= 0.32;
e19.. exp(-0.029595*x26)*(33.7894914681534 + x26) + x33 =E= 33.7894914681534;
e20.. exp(-0.029595*x26) + x34 =E= 1;
e21.. -0.134723681728774*(0.010073140669*x19**2 + 0.011394190823*x20**2 +
0.052910213683*x21**2 + 0.000159410872*x19*x20 + 0.008036404292*x19*x21
- 0.003423392047*x20*x21 + 0.097124049148*x19 + 0.03829180344*x20 +
0.370440556286*x21) + x31 =E= 0.29587368369345;
e22.. -0.134723681728774*(0.46598008632*x19**2 - 0.00797004615*x20**2 -
0.01779288613*x21**2 - 0.01429434551*x19*x20 - 0.03832188467*x19*x21 +
0.00970510229*x20*x21 - 0.88981702163*x19 + 0.07730602595*x20 +
0.39988032723*x21) + x32 =E= 0.194162178290626;
e23.. -(2715.7894736842/x27 + 5187*x31 - 5187*x32)*x26/(4320*x21 - 5187*x32)
+ x30 =E= 0;
e24.. exp(-0.029595*x30)*(33.7894914681534 + x30) + x35 =E= 33.7894914681534;
e25.. exp(-0.029595*x30) + x36 =E= 1;
e26.. exp(-0.029595*x44)*(33.7894914681534 + x44) + x51 =E= 33.7894914681534;
e27.. exp(-0.029595*x44) + x52 =E= 1;
e28.. -0.134723681728774*(0.010073140669*x37**2 + 0.011394190823*x38**2 +
0.052910213683*x39**2 + 0.000159410872*x37*x38 + 0.008036404292*x37*x39
- 0.003423392047*x38*x39 + 0.097124049148*x37 + 0.03829180344*x38 +
0.370440556286*x39) + x49 =E= 0.29587368369345;
e29.. -0.134723681728774*(0.46598008632*x37**2 - 0.00797004615*x38**2 -
0.01779288613*x39**2 - 0.01429434551*x37*x38 - 0.03832188467*x37*x39 +
0.00970510229*x38*x39 - 0.88981702163*x37 + 0.07730602595*x38 +
0.39988032723*x39) + x50 =E= 0.194162178290626;
e30.. -(2715.7894736842/x45 + 5187*x49 - 5187*x50)*x44/(4320*x39 - 5187*x50)
+ x48 =E= 0;
e31.. exp(-0.029595*x48)*(33.7894914681534 + x48) + x53 =E= 33.7894914681534;
e32.. exp(-0.029595*x48) + x54 =E= 1;
e33.. b1 + b2 + b3 =E= 1;
e34.. b1*x26 =L= 0;
e35.. b2*x26 =G= 0;
e36.. b2*(x26 - x55) =L= 0;
e37.. b3*(x26 - x55) =G= 0;
e38.. b4 + b5 + b6 =E= 1;
e39.. b4*x30 =L= 0;
e40.. b5*x30 =G= 0;
e41.. b5*(x30 - x55) =L= 0;
e42.. b6*(x30 - x55) =G= 0;
e43.. b3 + b5 =L= 1;
e44.. b4*(-1 + b1) =G= 0;
e45.. b7 + b8 + b9 =E= 1;
e46.. b7*(x44 - x55) =L= 0;
e47.. b8*(x44 - x55) =G= 0;
e48.. b8*(-200 + x44) =L= 0;
e49.. b9*(-200 + x44) =G= 0;
e50.. b10 + b11 + b12 =E= 1;
e51.. b10*(x48 - x55) =L= 0;
e52.. b11*(x48 - x55) =G= 0;
e53.. b11*(-200 + x48) =L= 0;
e54.. b12*(-200 + x48) =G= 0;
e55.. b9 + b11 =L= 1;
e56.. b10*(-1 + b7) =G= 0;
e57.. -(0.412152560083595*b15*x56 + 0.247360857459789*b14*x56 + ((11.34*x56/x28
+ (0.854659090909091/x27 - 11.34/x28)*x26*x57)*b1 + 0.0566666666666667*
x56 + (0.854659090909091*x33/x27 + (11.34*x56 - 11.34*x33)/x28 + (
0.854659090909091/x27 - 11.34/x28)*x26*(x57 - x34))*b2 +
0.854659090909091*x56/x27*b3 + 0.01728*b4*x21*x56 + b1*b5*(0.6*(0.03458*
x32*x35 + (0.0181052631578947/x27 + 0.03458*x31 - 0.03458*x32)*x26*x36)
+ 0.01728*x21*(x56 - x35)) + b2*b5*(0.6*((0.0181052631578947/x27 +
0.03458*x31)*x33 + 0.03458*x32*(x35 - x33) + (0.0181052631578947/x27 +
0.03458*x31 - 0.03458*x32)*x26*(x36 - x34)) + 0.01728*x21*(x56 - x35)) +
0.6*b1*b6*(0.03458*x32*x56 + (0.0181052631578947/x27 + 0.03458*x31 -
0.03458*x32)*x26*x57) + 0.6*b2*b6*((0.0181052631578947/x27 + 0.03458*x31)
*x33 + 0.03458*x32*(x56 - x33) + (0.0181052631578947/x27 + 0.03458*x31 -
0.03458*x32)*x26*(x57 - x34)) + 0.6*b3*b6*(0.0181052631578947/x27 +
0.03458*x31)*x56)*b13) + x29 =E= 0;
e58.. b13 + b14 + b15 =E= 1;
e59.. -(b18*(13.6674288800091 - 0.412152560083595*x56) + b17*(8.20275610163388
- 0.247360857459789*x56) + (1.87912853526074 + ((376.046780997472 -
11.34*x56)/x46 + (0.854659090909091/x45 - 11.34/x46)*x44*(
0.997312113279821 - x57))*b7 - 0.0566666666666667*x56 + ((
0.854659090909091*x51 - 0.854659090909091*x56)/x45 + (376.046780997472 -
11.34*x51)/x46 + (0.854659090909091/x45 - 11.34/x46)*x44*(
0.997312113279821 - x52))*b8 + (28.341428570246 - 0.854659090909091*x56)/
x45*b9 + 0.01728*b10*x39*(33.1610917987189 - x56) + b7*b11*(0.6*(0.03458*
x50*(x53 - x56) + (0.0181052631578947/x45 + 0.03458*x49 - 0.03458*x50)*
x44*(x54 - x57)) + 0.01728*x39*(33.1610917987189 - x53)) + b8*b11*(0.6*((
0.0181052631578947/x45 + 0.03458*x49)*(x51 - x56) + 0.03458*x50*(x53 -
x51) + (0.0181052631578947/x45 + 0.03458*x49 - 0.03458*x50)*x44*(x54 -
x52)) + 0.01728*x39*(33.1610917987189 - x53)) + 0.6*b7*b12*(0.03458*x50*(
33.1610917987189 - x56) + (0.0181052631578947/x45 + 0.03458*x49 - 0.03458
*x50)*x44*(0.997312113279821 - x57)) + 0.6*b8*b12*((0.0181052631578947/
x45 + 0.03458*x49)*(x51 - x56) + 0.03458*x50*(33.1610917987189 - x51) + (
0.0181052631578947/x45 + 0.03458*x49 - 0.03458*x50)*x44*(
0.997312113279821 - x52)) + 0.6*b9*b12*(0.0181052631578947/x45 + 0.03458*
x49)*(33.1610917987189 - x56))*b16) + x47 =E= 0;
e60.. b16 + b17 + b18 =E= 1;
e61.. - x29 - x47 + objvar =E= 0;
e62.. exp(-0.029595*x55)*(33.7894914681534 + x55) + x56 =E= 33.7894914681534;
e63.. exp(-0.029595*x55) + x57 =E= 1;
* set non-default bounds
x19.lo = 0.526315789473684; x19.up = 1.05263157894737;
x20.lo = 0.961538461538462; x20.up = 2.11538461538462;
x21.lo = 0.2; x21.up = 1;
x22.up = 0.8;
x23.lo = 6; x23.up = 13;
x24.lo = 6; x24.up = 13;
x25.lo = 0.26; x25.up = 0.35;
x26.up = 90;
x27.lo = 4.9; x27.up = 5.5;
x28.lo = 55; x28.up = 63;
x30.up = 200;
x31.lo = 0.296392099803303; x31.up = 0.404171045186323;
x32.lo = 0.134723681728774; x32.up = 0.229030258938916;
x33.up = 26;
x34.up = 1;
x35.up = 34.1;
x36.up = 1;
x37.lo = 0.526315789473684; x37.up = 1.05263157894737;
x38.lo = 0.961538461538462; x38.up = 2.11538461538462;
x39.lo = 0.2; x39.up = 1;
x40.up = 0.8;
x41.lo = 6; x41.up = 13;
x42.lo = 6; x42.up = 13;
x43.lo = 0.26; x43.up = 0.35;
x44.up = 90;
x45.lo = 4.9; x45.up = 5.5;
x46.lo = 55; x46.up = 63;
x48.up = 200;
x49.lo = 0.296392099803303; x49.up = 0.404171045186323;
x50.lo = 0.134723681728774; x50.up = 0.229030258938916;
x51.up = 26;
x52.up = 1;
x53.up = 34.1;
x54.up = 1;
x55.up = 200;
x56.up = 34.1;
x57.up = 1;
* set non-default levels
b2.l = 1;
b5.l = 1;
b7.l = 1;
b11.l = 1;
b13.l = 1;
b16.l = 1;
x19.l = 1;
x20.l = 1;
x21.l = 0.3;
x22.l = 0.8;
x23.l = 13;
x24.l = 10.6604143883993;
x25.l = 0.3273636888081;
x26.l = 27.4760701692312;
x27.l = 5.30016785671899;
x28.l = 58.4294759668997;
x30.l = 82.6048888012009;
x31.l = 0.332831162843986;
x32.l = 0.159266373947579;
x33.l = 6.62084546202556;
x34.l = 0.556542937336767;
x35.l = 23.6919439882642;
x36.l = 0.913247121927004;
x37.l = 0.8;
x39.l = 0.4;
x40.l = 0.8;
x41.l = 13;
x42.l = 12.0499480711157;
x43.l = 0.31546674627608;
x44.l = 36.408786197323;
x45.l = 5.26747485493678;
x46.l = 59.9333303564984;
x48.l = 58.2740173254705;
x49.l = 0.334395741702399;
x50.l = 0.165538447790303;
x51.l = 9.8912291834487;
x52.l = 0.659560560750654;
x53.l = 17.380013231931;
x54.l = 0.821759148100612;
x55.l = 30;
x56.l = 7.53758887227811;
x57.l = 0.588460387570554;
Model m / all /;
m.limrow=0; m.limcol=0;
m.tolproj=0.0;
$if NOT '%gams.u1%' == '' $include '%gams.u1%'
$if not set MINLP $set MINLP MINLP
Solve m using %MINLP% minimizing objvar;
Last updated: 2025-08-07 Git hash: e62cedfc