MINLPLib
A Library of Mixed-Integer and Continuous Nonlinear Programming Instances
Home // Instances // Documentation // Download // Statistics
Instance p_ball_10b_5p_2d_m
Select 5-points in 2-dimensional balls, such that the l1-distance between all points is minimized. Only one point can be assigned to each ball, and in total there are 10 balls with radius one. This is a big-M formulation.
| Formatsⓘ | ams gms lp mod nl osil pip py |
| Primal Bounds (infeas ≤ 1e-08)ⓘ | |
| Other points (infeas > 1e-08)ⓘ | |
| Dual Boundsⓘ | 18.71737986 (ALPHAECP) 18.71848326 (ANTIGONE) 18.71857768 (BARON) 18.71857793 (BONMIN) 18.71855872 (COUENNE) 18.71857799 (CPLEX) 18.71854375 (GUROBI) 18.71857799 (LINDO) 18.71857511 (SCIP) 18.71857799 (SHOT) |
| Referencesⓘ | Kronqvist, Jan and Misener, Ruth, A disjunctive cut strengthening technique for convex MINLP, Tech. Rep., 2020. |
| Sourceⓘ | p_ball_10b_5p_2d.gms, contributed by Jan Kronqvist and Ruth Misener |
| Applicationⓘ | Geometry |
| Added to libraryⓘ | 26 Aug 2020 |
| Problem typeⓘ | MBQCP |
| #Variablesⓘ | 80 |
| #Binary Variablesⓘ | 50 |
| #Integer Variablesⓘ | 0 |
| #Nonlinear Variablesⓘ | 10 |
| #Nonlinear Binary Variablesⓘ | 0 |
| #Nonlinear Integer Variablesⓘ | 0 |
| Objective Senseⓘ | min |
| Objective typeⓘ | linear |
| Objective curvatureⓘ | linear |
| #Nonzeros in Objectiveⓘ | 20 |
| #Nonlinear Nonzeros in Objectiveⓘ | 0 |
| #Constraintsⓘ | 109 |
| #Linear Constraintsⓘ | 59 |
| #Quadratic Constraintsⓘ | 50 |
| #Polynomial Constraintsⓘ | 0 |
| #Signomial Constraintsⓘ | 0 |
| #General Nonlinear Constraintsⓘ | 0 |
| Operands in Gen. Nonlin. Functionsⓘ | |
| Constraints curvatureⓘ | convex |
| #Nonzeros in Jacobianⓘ | 378 |
| #Nonlinear Nonzeros in Jacobianⓘ | 100 |
| #Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ | 10 |
| #Nonzeros in Diagonal of Hessian of Lagrangianⓘ | 10 |
| #Blocks in Hessian of Lagrangianⓘ | 10 |
| Minimal blocksize in Hessian of Lagrangianⓘ | 1 |
| Maximal blocksize in Hessian of Lagrangianⓘ | 1 |
| Average blocksize in Hessian of Lagrangianⓘ | 1.0 |
| #Semicontinuitiesⓘ | 0 |
| #Nonlinear Semicontinuitiesⓘ | 0 |
| #SOS type 1ⓘ | 0 |
| #SOS type 2ⓘ | 0 |
| Minimal coefficientⓘ | 3.8028e-01 |
| Maximal coefficientⓘ | 1.2038e+02 |
| Infeasibility of initial pointⓘ | 7.83e-05 |
| Sparsity Jacobianⓘ | 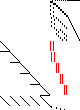 |
| Sparsity Hessian of Lagrangianⓘ |  |
$offlisting
*
* Equation counts
* Total E G L N X C B
* 110 6 0 104 0 0 0 0
*
* Variable counts
* x b i s1s s2s sc si
* Total cont binary integer sos1 sos2 scont sint
* 81 31 50 0 0 0 0 0
* FX 0
*
* Nonzero counts
* Total const NL DLL
* 399 299 100 0
*
* Solve m using MINLP minimizing objvar;
Variables b1,b2,b3,b4,b5,b6,b7,b8,b9,b10,b11,b12,b13,b14,b15,b16,b17,b18,b19
,b20,b21,b22,b23,b24,b25,b26,b27,b28,b29,b30,b31,b32,b33,b34,b35,b36
,b37,b38,b39,b40,b41,b42,b43,b44,b45,b46,b47,b48,b49,b50,x51,x52,x53
,x54,x55,x56,x57,x58,x59,x60,x61,x62,x63,x64,x65,x66,x67,x68,x69,x70
,x71,x72,x73,x74,x75,x76,x77,x78,x79,x80,objvar;
Positive Variables x51,x52,x53,x54,x55,x56,x57,x58,x59,x60,x61,x62,x63,x64
,x65,x66,x67,x68,x69,x70,x71,x72,x73,x74,x75,x76,x77,x78,x79,x80;
Binary Variables b1,b2,b3,b4,b5,b6,b7,b8,b9,b10,b11,b12,b13,b14,b15,b16,b17
,b18,b19,b20,b21,b22,b23,b24,b25,b26,b27,b28,b29,b30,b31,b32,b33,b34
,b35,b36,b37,b38,b39,b40,b41,b42,b43,b44,b45,b46,b47,b48,b49,b50;
Equations e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13,e14,e15,e16,e17,e18,e19
,e20,e21,e22,e23,e24,e25,e26,e27,e28,e29,e30,e31,e32,e33,e34,e35,e36
,e37,e38,e39,e40,e41,e42,e43,e44,e45,e46,e47,e48,e49,e50,e51,e52,e53
,e54,e55,e56,e57,e58,e59,e60,e61,e62,e63,e64,e65,e66,e67,e68,e69,e70
,e71,e72,e73,e74,e75,e76,e77,e78,e79,e80,e81,e82,e83,e84,e85,e86,e87
,e88,e89,e90,e91,e92,e93,e94,e95,e96,e97,e98,e99,e100,e101,e102,e103
,e104,e105,e106,e107,e108,e109,e110;
e1.. x51 - x52 - x53 =L= 0;
e2.. - x51 + x52 - x53 =L= 0;
e3.. x54 - x55 - x56 =L= 0;
e4.. - x54 + x55 - x56 =L= 0;
e5.. x51 - x57 - x58 =L= 0;
e6.. - x51 + x57 - x58 =L= 0;
e7.. x54 - x59 - x60 =L= 0;
e8.. - x54 + x59 - x60 =L= 0;
e9.. x51 - x61 - x62 =L= 0;
e10.. - x51 + x61 - x62 =L= 0;
e11.. x54 - x63 - x64 =L= 0;
e12.. - x54 + x63 - x64 =L= 0;
e13.. x51 - x65 - x66 =L= 0;
e14.. - x51 + x65 - x66 =L= 0;
e15.. x54 - x67 - x68 =L= 0;
e16.. - x54 + x67 - x68 =L= 0;
e17.. x52 - x57 - x69 =L= 0;
e18.. - x52 + x57 - x69 =L= 0;
e19.. x55 - x59 - x70 =L= 0;
e20.. - x55 + x59 - x70 =L= 0;
e21.. x52 - x61 - x71 =L= 0;
e22.. - x52 + x61 - x71 =L= 0;
e23.. x55 - x63 - x72 =L= 0;
e24.. - x55 + x63 - x72 =L= 0;
e25.. x52 - x65 - x73 =L= 0;
e26.. - x52 + x65 - x73 =L= 0;
e27.. x55 - x67 - x74 =L= 0;
e28.. - x55 + x67 - x74 =L= 0;
e29.. x57 - x61 - x75 =L= 0;
e30.. - x57 + x61 - x75 =L= 0;
e31.. x59 - x63 - x76 =L= 0;
e32.. - x59 + x63 - x76 =L= 0;
e33.. x57 - x65 - x77 =L= 0;
e34.. - x57 + x65 - x77 =L= 0;
e35.. x59 - x67 - x78 =L= 0;
e36.. - x59 + x67 - x78 =L= 0;
e37.. x61 - x65 - x79 =L= 0;
e38.. - x61 + x65 - x79 =L= 0;
e39.. x63 - x67 - x80 =L= 0;
e40.. - x63 + x67 - x80 =L= 0;
e41.. sqr(0.648386267690458 - x51) + sqr(5.34198386756466 - x54)
+ 109.233018040634*b1 =L= 110.233018040634;
e42.. sqr(0.38028139143083 - x51) + sqr(4.79200736168083 - x54)
+ 108.933937361066*b2 =L= 109.933937361066;
e43.. sqr(4.59553989190787 - x51) + sqr(2.92927044373959 - x54)
+ 54.6585416851302*b3 =L= 55.6585416851302;
e44.. sqr(7.79089239319392 - x51) + sqr(3.09688601355012 - x54)
+ 72.9946165089168*b4 =L= 73.9946165089168;
e45.. sqr(2.20597420581599 - x51) + sqr(0.880296019425143 - x54)
+ 103.212034038779*b5 =L= 104.212034038779;
e46.. sqr(4.31093077060147 - x51) + sqr(5.42555328385657 - x54)
+ 56.8881542099775*b6 =L= 57.8881542099775;
e47.. sqr(8.68776252232421 - x51) + sqr(7.42106012944621 - x54)
+ 103.212034038779*b7 =L= 104.212034038779;
e48.. sqr(3.86794113528858 - x51) + sqr(9.34863265837716 - x54)
+ 120.378073325993*b8 =L= 121.378073325993;
e49.. sqr(8.94294324678777 - x51) + sqr(0.712193380632226 - x54)
+ 120.378073325993*b9 =L= 121.378073325993;
e50.. sqr(1.56734614217404 - x51) + sqr(5.6469805099144 - x54)
+ 96.4999714251602*b10 =L= 97.4999714251602;
e51.. b1 + b2 + b3 + b4 + b5 + b6 + b7 + b8 + b9 + b10 =E= 1;
e52.. sqr(0.648386267690458 - x52) + sqr(5.34198386756466 - x55)
+ 109.233018040634*b11 =L= 110.233018040634;
e53.. sqr(0.38028139143083 - x52) + sqr(4.79200736168083 - x55)
+ 108.933937361066*b12 =L= 109.933937361066;
e54.. sqr(4.59553989190787 - x52) + sqr(2.92927044373959 - x55)
+ 54.6585416851302*b13 =L= 55.6585416851302;
e55.. sqr(7.79089239319392 - x52) + sqr(3.09688601355012 - x55)
+ 72.9946165089168*b14 =L= 73.9946165089168;
e56.. sqr(2.20597420581599 - x52) + sqr(0.880296019425143 - x55)
+ 103.212034038779*b15 =L= 104.212034038779;
e57.. sqr(4.31093077060147 - x52) + sqr(5.42555328385657 - x55)
+ 56.8881542099775*b16 =L= 57.8881542099775;
e58.. sqr(8.68776252232421 - x52) + sqr(7.42106012944621 - x55)
+ 103.212034038779*b17 =L= 104.212034038779;
e59.. sqr(3.86794113528858 - x52) + sqr(9.34863265837716 - x55)
+ 120.378073325993*b18 =L= 121.378073325993;
e60.. sqr(8.94294324678777 - x52) + sqr(0.712193380632226 - x55)
+ 120.378073325993*b19 =L= 121.378073325993;
e61.. sqr(1.56734614217404 - x52) + sqr(5.6469805099144 - x55)
+ 96.4999714251602*b20 =L= 97.4999714251602;
e62.. b11 + b12 + b13 + b14 + b15 + b16 + b17 + b18 + b19 + b20 =E= 1;
e63.. sqr(0.648386267690458 - x57) + sqr(5.34198386756466 - x59)
+ 109.233018040634*b21 =L= 110.233018040634;
e64.. sqr(0.38028139143083 - x57) + sqr(4.79200736168083 - x59)
+ 108.933937361066*b22 =L= 109.933937361066;
e65.. sqr(4.59553989190787 - x57) + sqr(2.92927044373959 - x59)
+ 54.6585416851302*b23 =L= 55.6585416851302;
e66.. sqr(7.79089239319392 - x57) + sqr(3.09688601355012 - x59)
+ 72.9946165089168*b24 =L= 73.9946165089168;
e67.. sqr(2.20597420581599 - x57) + sqr(0.880296019425143 - x59)
+ 103.212034038779*b25 =L= 104.212034038779;
e68.. sqr(4.31093077060147 - x57) + sqr(5.42555328385657 - x59)
+ 56.8881542099775*b26 =L= 57.8881542099775;
e69.. sqr(8.68776252232421 - x57) + sqr(7.42106012944621 - x59)
+ 103.212034038779*b27 =L= 104.212034038779;
e70.. sqr(3.86794113528858 - x57) + sqr(9.34863265837716 - x59)
+ 120.378073325993*b28 =L= 121.378073325993;
e71.. sqr(8.94294324678777 - x57) + sqr(0.712193380632226 - x59)
+ 120.378073325993*b29 =L= 121.378073325993;
e72.. sqr(1.56734614217404 - x57) + sqr(5.6469805099144 - x59)
+ 96.4999714251602*b30 =L= 97.4999714251602;
e73.. b21 + b22 + b23 + b24 + b25 + b26 + b27 + b28 + b29 + b30 =E= 1;
e74.. sqr(0.648386267690458 - x61) + sqr(5.34198386756466 - x63)
+ 109.233018040634*b31 =L= 110.233018040634;
e75.. sqr(0.38028139143083 - x61) + sqr(4.79200736168083 - x63)
+ 108.933937361066*b32 =L= 109.933937361066;
e76.. sqr(4.59553989190787 - x61) + sqr(2.92927044373959 - x63)
+ 54.6585416851302*b33 =L= 55.6585416851302;
e77.. sqr(7.79089239319392 - x61) + sqr(3.09688601355012 - x63)
+ 72.9946165089168*b34 =L= 73.9946165089168;
e78.. sqr(2.20597420581599 - x61) + sqr(0.880296019425143 - x63)
+ 103.212034038779*b35 =L= 104.212034038779;
e79.. sqr(4.31093077060147 - x61) + sqr(5.42555328385657 - x63)
+ 56.8881542099775*b36 =L= 57.8881542099775;
e80.. sqr(8.68776252232421 - x61) + sqr(7.42106012944621 - x63)
+ 103.212034038779*b37 =L= 104.212034038779;
e81.. sqr(3.86794113528858 - x61) + sqr(9.34863265837716 - x63)
+ 120.378073325993*b38 =L= 121.378073325993;
e82.. sqr(8.94294324678777 - x61) + sqr(0.712193380632226 - x63)
+ 120.378073325993*b39 =L= 121.378073325993;
e83.. sqr(1.56734614217404 - x61) + sqr(5.6469805099144 - x63)
+ 96.4999714251602*b40 =L= 97.4999714251602;
e84.. b31 + b32 + b33 + b34 + b35 + b36 + b37 + b38 + b39 + b40 =E= 1;
e85.. sqr(0.648386267690458 - x65) + sqr(5.34198386756466 - x67)
+ 109.233018040634*b41 =L= 110.233018040634;
e86.. sqr(0.38028139143083 - x65) + sqr(4.79200736168083 - x67)
+ 108.933937361066*b42 =L= 109.933937361066;
e87.. sqr(4.59553989190787 - x65) + sqr(2.92927044373959 - x67)
+ 54.6585416851302*b43 =L= 55.6585416851302;
e88.. sqr(7.79089239319392 - x65) + sqr(3.09688601355012 - x67)
+ 72.9946165089168*b44 =L= 73.9946165089168;
e89.. sqr(2.20597420581599 - x65) + sqr(0.880296019425143 - x67)
+ 103.212034038779*b45 =L= 104.212034038779;
e90.. sqr(4.31093077060147 - x65) + sqr(5.42555328385657 - x67)
+ 56.8881542099775*b46 =L= 57.8881542099775;
e91.. sqr(8.68776252232421 - x65) + sqr(7.42106012944621 - x67)
+ 103.212034038779*b47 =L= 104.212034038779;
e92.. sqr(3.86794113528858 - x65) + sqr(9.34863265837716 - x67)
+ 120.378073325993*b48 =L= 121.378073325993;
e93.. sqr(8.94294324678777 - x65) + sqr(0.712193380632226 - x67)
+ 120.378073325993*b49 =L= 121.378073325993;
e94.. sqr(1.56734614217404 - x65) + sqr(5.6469805099144 - x67)
+ 96.4999714251602*b50 =L= 97.4999714251602;
e95.. b41 + b42 + b43 + b44 + b45 + b46 + b47 + b48 + b49 + b50 =E= 1;
e96.. b1 + b11 + b21 + b31 + b41 =L= 1;
e97.. b2 + b12 + b22 + b32 + b42 =L= 1;
e98.. b3 + b13 + b23 + b33 + b43 =L= 1;
e99.. b4 + b14 + b24 + b34 + b44 =L= 1;
e100.. b5 + b15 + b25 + b35 + b45 =L= 1;
e101.. b6 + b16 + b26 + b36 + b46 =L= 1;
e102.. b7 + b17 + b27 + b37 + b47 =L= 1;
e103.. b8 + b18 + b28 + b38 + b48 =L= 1;
e104.. b9 + b19 + b29 + b39 + b49 =L= 1;
e105.. b10 + b20 + b30 + b40 + b50 =L= 1;
e106.. x51 - x52 =L= 0;
e107.. x52 - x57 =L= 0;
e108.. x57 - x61 =L= 0;
e109.. x61 - x65 =L= 0;
e110.. - x53 - x56 - x58 - x60 - x62 - x64 - x66 - x68 - x69 - x70 - x71 - x72
- x73 - x74 - x75 - x76 - x77 - x78 - x79 - x80 + objvar =E= 0;
* set non-default bounds
x51.up = 10;
x52.up = 10;
x53.up = 10;
x54.up = 10;
x55.up = 10;
x56.up = 10;
x57.up = 10;
x58.up = 10;
x59.up = 10;
x60.up = 10;
x61.up = 10;
x62.up = 10;
x63.up = 10;
x64.up = 10;
x65.up = 10;
x66.up = 10;
x67.up = 10;
x68.up = 10;
x69.up = 10;
x70.up = 10;
x71.up = 10;
x72.up = 10;
x73.up = 10;
x74.up = 10;
x75.up = 10;
x76.up = 10;
x77.up = 10;
x78.up = 10;
x79.up = 10;
x80.up = 10;
* set non-default levels
b2.l = 1;
b11.l = 1;
b30.l = 1;
b36.l = 1;
b43.l = 1;
x51.l = 1.37695009606239;
x52.l = 1.42378547420432;
x53.l = 0.0468353781419294;
x54.l = 4.71045051597106;
x55.l = 4.71045051597106;
x57.l = 1.91800199645783;
x58.l = 0.541051900395441;
x59.l = 4.71045051597106;
x61.l = 3.61191140798068;
x62.l = 2.23496131191829;
x63.l = 4.71045051597106;
x65.l = 3.89283484794216;
x66.l = 2.51588475187977;
x67.l = 3.64078525445372;
x68.l = 1.06966526151734;
x69.l = 0.494216522253511;
x71.l = 2.18812593377636;
x73.l = 2.46904937373784;
x74.l = 1.06966526151734;
x75.l = 1.69390941152285;
x77.l = 1.97483285148432;
x78.l = 1.06966526151734;
x79.l = 0.280923439961476;
x80.l = 1.06966526151734;
Model m / all /;
m.limrow=0; m.limcol=0;
m.tolproj=0.0;
$if NOT '%gams.u1%' == '' $include '%gams.u1%'
$if not set MINLP $set MINLP MINLP
Solve m using %MINLP% minimizing objvar;
Last updated: 2025-08-07 Git hash: e62cedfc