MINLPLib
A Library of Mixed-Integer and Continuous Nonlinear Programming Instances
Home // Instances // Documentation // Download // Statistics
Instance prolog
| Formatsⓘ | ams gms lp mod nl osil pip py |
| Primal Bounds (infeas ≤ 1e-08)ⓘ | |
| Other points (infeas > 1e-08)ⓘ | |
| Dual Boundsⓘ | -0.00000000 (ANTIGONE) 0.00000000 (BARON) -0.00000000 (COUENNE) 0.00000000 (GUROBI) 0.00000000 (LINDO) 0.00000000 (SCIP) |
| Referencesⓘ | Norton, R D and Scandizzo, P L, Market Equilibrium Computations in Activity Analysis Models, Operations Research, 29:2, 1981, 243-262. |
| Sourceⓘ | GAMS Model Library model prolog |
| Applicationⓘ | Market Equilibrium |
| Added to libraryⓘ | 31 Jul 2001 |
| Problem typeⓘ | QCQP |
| #Variablesⓘ | 20 |
| #Binary Variablesⓘ | 0 |
| #Integer Variablesⓘ | 0 |
| #Nonlinear Variablesⓘ | 6 |
| #Nonlinear Binary Variablesⓘ | 0 |
| #Nonlinear Integer Variablesⓘ | 0 |
| Objective Senseⓘ | min |
| Objective typeⓘ | quadratic |
| Objective curvatureⓘ | indefinite |
| #Nonzeros in Objectiveⓘ | 8 |
| #Nonlinear Nonzeros in Objectiveⓘ | 6 |
| #Constraintsⓘ | 22 |
| #Linear Constraintsⓘ | 20 |
| #Quadratic Constraintsⓘ | 2 |
| #Polynomial Constraintsⓘ | 0 |
| #Signomial Constraintsⓘ | 0 |
| #General Nonlinear Constraintsⓘ | 0 |
| Operands in Gen. Nonlin. Functionsⓘ | |
| Constraints curvatureⓘ | indefinite |
| #Nonzeros in Jacobianⓘ | 120 |
| #Nonlinear Nonzeros in Jacobianⓘ | 8 |
| #Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ | 8 |
| #Nonzeros in Diagonal of Hessian of Lagrangianⓘ | 0 |
| #Blocks in Hessian of Lagrangianⓘ | 2 |
| Minimal blocksize in Hessian of Lagrangianⓘ | 3 |
| Maximal blocksize in Hessian of Lagrangianⓘ | 3 |
| Average blocksize in Hessian of Lagrangianⓘ | 3.0 |
| #Semicontinuitiesⓘ | 0 |
| #Nonlinear Semicontinuitiesⓘ | 0 |
| #SOS type 1ⓘ | 0 |
| #SOS type 2ⓘ | 0 |
| Minimal coefficientⓘ | 4.8000e-02 |
| Maximal coefficientⓘ | 5.0000e+03 |
| Infeasibility of initial pointⓘ | 782 |
| Sparsity Jacobianⓘ | 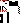 |
| Sparsity Hessian of Lagrangianⓘ | 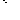 |
$offlisting
*
* Equation counts
* Total E G L N X C B
* 23 1 0 22 0 0 0 0
*
* Variable counts
* x b i s1s s2s sc si
* Total cont binary integer sos1 sos2 scont sint
* 21 21 0 0 0 0 0 0
* FX 0
*
* Nonzero counts
* Total const NL DLL
* 129 115 14 0
*
* Solve m using NLP minimizing objvar;
Variables objvar,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18
,x19,x20,x21;
Positive Variables x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19,x20
,x21;
Equations e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13,e14,e15,e16,e17,e18,e19
,e20,e21,e22,e23;
e1.. x5 + x6 - 0.94*x11 - 0.94*x12 - 0.94*x13 + 0.244*x17 + 0.244*x18
+ 0.244*x19 =L= 0;
e2.. 0.064*x11 + 0.064*x12 + 0.064*x13 - 0.58*x14 - 0.58*x15 - 0.58*x16
+ 0.172*x17 + 0.172*x18 + 0.172*x19 =L= 0;
e3.. x7 + x8 + 0.048*x11 + 0.048*x12 + 0.048*x13 + 0.247*x14 + 0.247*x15
+ 0.247*x16 - 0.916*x17 - 0.916*x18 - 0.916*x19 =L= 0;
e4.. x11 + 1.2*x12 + 0.8*x13 + 2*x14 + 1.8*x15 + 2.4*x16 + 3*x17 + 2.7*x18
+ 3.2*x19 =L= 3712;
e5.. 2*x11 + 1.8*x12 + 2.2*x13 + 3*x14 + 3.5*x15 + 2.3*x16 + 3*x17 + 3.2*x18
+ 2.7*x19 =L= 5000;
e6.. 356.474947137148*x2 + 53.7083537310174*x4 + x5 - 0.564264890180399*x20
=L= 352;
e7.. 339.983422262764*x2 + 43.5418249774113*x4 + x6 - 0.405939876920766*x21
=L= 430;
e8.. 106.946746119538*x2 + 145.018955433089*x4 + x7 - 0.507117039797071*x20
=L= 222;
e9.. 173.929713444361*x2 + 203.031384299627*x4 + x8 - 0.578889145413521*x21
=L= 292;
e10.. x5*x2 + x7*x4 - x20 =L= 0;
e11.. x6*x2 + x8*x4 - x21 =L= 0;
e12.. - 3340.8*x9 - 500*x10 + x20 =L= 0;
e13.. - 371.2*x9 - 4500*x10 + x21 =L= 0;
e14.. 0.94*x2 - 0.064*x3 - 0.048*x4 - x9 - 2*x10 =L= 0;
e15.. 0.94*x2 - 0.064*x3 - 0.048*x4 - 1.2*x9 - 1.8*x10 =L= 0;
e16.. 0.94*x2 - 0.064*x3 - 0.048*x4 - 0.8*x9 - 2.2*x10 =L= 0;
e17.. 0.58*x3 - 0.247*x4 - 2*x9 - 3*x10 =L= 0;
e18.. 0.58*x3 - 0.247*x4 - 1.8*x9 - 3.5*x10 =L= 0;
e19.. 0.58*x3 - 0.247*x4 - 2.4*x9 - 2.3*x10 =L= 0;
e20.. - 0.244*x2 - 0.172*x3 + 0.916*x4 - 3*x9 - 3*x10 =L= 0;
e21.. - 0.244*x2 - 0.172*x3 + 0.916*x4 - 2.7*x9 - 3.2*x10 =L= 0;
e22.. - 0.244*x2 - 0.172*x3 + 0.916*x4 - 3.2*x9 - 2.7*x10 =L= 0;
e23.. -(x5*x2 + x6*x2 + x7*x4 + x8*x4) - objvar + 3712*x9 + 5000*x10 =E= 0;
* set non-default bounds
x2.lo = 0.2;
x3.lo = 0.2;
x4.lo = 0.2;
* set non-default levels
x2.l = 0.5942;
x3.l = 1.6167;
x4.l = 1.31077;
x5.l = 352;
x6.l = 430;
x7.l = 222;
x8.l = 292;
x9.l = 0.130670360422406;
x10.l = 0.130670360422406;
x20.l = 500.14934;
x21.l = 638.25084;
Model m / all /;
m.limrow=0; m.limcol=0;
m.tolproj=0.0;
$if NOT '%gams.u1%' == '' $include '%gams.u1%'
$if not set NLP $set NLP NLP
Solve m using %NLP% minimizing objvar;
Last updated: 2025-08-07 Git hash: e62cedfc