MINLPLib
A Library of Mixed-Integer and Continuous Nonlinear Programming Instances
Home // Instances // Documentation // Download // Statistics
Instance sfacloc1_2_95
Probabilistic Facility Location and Assignment with Random Demand (given by 5000 scenarios), where 2 facilities can be opened anywhere in the Euclidean plane (distances are measured with the Manhattan (or L1) metric), the facilities are capacitated and each customer may be served by more than one facility. The objective is to minimize an upper-bound on the weighted total-distance (i.e., the sum of the product of the demand of each customer times the distance to the facility serving that customer) such that this bound is satisfied with a reliability level of 0.95.
| Formatsⓘ | ams gms mod nl osil pip py |
| Primal Bounds (infeas ≤ 1e-08)ⓘ | |
| Other points (infeas > 1e-08)ⓘ | |
| Dual Boundsⓘ | 14.04268672 (ANTIGONE) 12.04156576 (BARON) 10.92901718 (COUENNE) 18.84994852 (GUROBI) 15.24662891 (LINDO) 15.77308569 (SCIP) 0.00000000 (SHOT) 18.85002998 (XPRESS) |
| Referencesⓘ | Lejeune, M A and Margot, François, Solving Chance-Constrained Optimization Problems with Stochastic Quadratic Inequalities, Operations Research, 64:4, 2016, 939-957. |
| Sourceⓘ | instance CCFACLOC/1B2C/M2_2/M2_2_1B2C_15_2_95_5000.nl from François Margot stochastic instances collection |
| Applicationⓘ | Facility Location |
| Added to libraryⓘ | 12 Aug 2014 |
| Problem typeⓘ | MBNLP |
| #Variablesⓘ | 171 |
| #Binary Variablesⓘ | 9 |
| #Integer Variablesⓘ | 0 |
| #Nonlinear Variablesⓘ | 68 |
| #Nonlinear Binary Variablesⓘ | 0 |
| #Nonlinear Integer Variablesⓘ | 0 |
| Objective Senseⓘ | min |
| Objective typeⓘ | linear |
| Objective curvatureⓘ | linear |
| #Nonzeros in Objectiveⓘ | 15 |
| #Nonlinear Nonzeros in Objectiveⓘ | 0 |
| #Constraintsⓘ | 208 |
| #Linear Constraintsⓘ | 193 |
| #Quadratic Constraintsⓘ | 7 |
| #Polynomial Constraintsⓘ | 8 |
| #Signomial Constraintsⓘ | 0 |
| #General Nonlinear Constraintsⓘ | 0 |
| Operands in Gen. Nonlin. Functionsⓘ | |
| Constraints curvatureⓘ | indefinite |
| #Nonzeros in Jacobianⓘ | 526 |
| #Nonlinear Nonzeros in Jacobianⓘ | 68 |
| #Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ | 124 |
| #Nonzeros in Diagonal of Hessian of Lagrangianⓘ | 0 |
| #Blocks in Hessian of Lagrangianⓘ | 22 |
| Minimal blocksize in Hessian of Lagrangianⓘ | 2 |
| Maximal blocksize in Hessian of Lagrangianⓘ | 5 |
| Average blocksize in Hessian of Lagrangianⓘ | 3.090909 |
| #Semicontinuitiesⓘ | 0 |
| #Nonlinear Semicontinuitiesⓘ | 0 |
| #SOS type 1ⓘ | 0 |
| #SOS type 2ⓘ | 0 |
| Minimal coefficientⓘ | 2.8000e-01 |
| Maximal coefficientⓘ | 9.9280e+01 |
| Infeasibility of initial pointⓘ | 94.77 |
| Sparsity Jacobianⓘ | 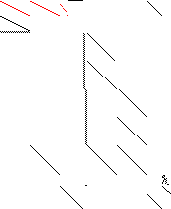 |
| Sparsity Hessian of Lagrangianⓘ |  |
$offlisting
*
* Equation counts
* Total E G L N X C B
* 209 69 123 17 0 0 0 0
*
* Variable counts
* x b i s1s s2s sc si
* Total cont binary integer sos1 sos2 scont sint
* 172 163 9 0 0 0 0 0
* FX 0
*
* Nonzero counts
* Total const NL DLL
* 542 474 68 0
*
* Solve m using MINLP minimizing objvar;
Variables x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19
,x20,x21,x22,x23,x24,x25,x26,x27,x28,x29,x30,x31,x32,x33,x34,x35,x36
,x37,x38,x39,x40,x41,x42,x43,x44,x45,x46,x47,x48,x49,x50,x51,x52,x53
,x54,x55,x56,x57,x58,x59,x60,x61,x62,x63,x64,x65,x66,x67,x68,x69,x70
,x71,x72,x73,x74,x75,x76,x77,x78,x79,x80,x81,x82,x83,x84,x85,x86,x87
,x88,x89,x90,x91,x92,x93,x94,x95,x96,x97,x98,x99,x100,x101,x102,x103
,x104,x105,x106,x107,x108,x109,x110,x111,x112,x113,x114,x115,x116
,x117,x118,x119,x120,x121,x122,x123,x124,x125,x126,x127,x128,x129
,x130,x131,x132,x133,x134,x135,x136,x137,x138,x139,x140,x141,x142
,x143,x144,x145,x146,x147,x148,x149,x150,x151,x152,x153,x154,x155
,x156,x157,x158,x159,x160,x161,x162,b163,b164,b165,b166,b167,b168
,b169,b170,b171,objvar;
Positive Variables x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17
,x18,x19,x20,x21,x22,x23,x24,x25,x26,x27,x28,x29,x30,x31,x32,x33,x34
,x35,x36,x37,x38,x39,x40,x41,x42,x43,x44,x45,x46,x47,x48,x49,x50,x51
,x52,x53,x54,x55,x56,x57,x58,x59,x60,x61,x62,x63,x64,x65,x66,x67,x68
,x69,x70,x71,x72,x73,x74,x75,x76,x77,x78,x79,x80,x81,x82,x83,x88,x89
,x90,x91,x92,x93,x94,x95,x96,x97,x98,x99,x100,x101,x102,x103,x104
,x105,x106,x107,x108,x109,x110,x111,x112,x113,x114,x115,x116,x117
,x118,x119,x120,x121,x122,x123,x124,x125,x126,x127,x128,x129,x130
,x131,x132,x133,x134,x135,x136,x137,x138,x139,x140,x141,x142,x143
,x144,x145,x146,x147,x148,x149,x150,x151,x152,x153,x154,x155,x156
,x157,x158,x159,x160,x161,x162;
Binary Variables b163,b164,b165,b166,b167,b168,b169,b170,b171;
Equations e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13,e14,e15,e16,e17,e18,e19
,e20,e21,e22,e23,e24,e25,e26,e27,e28,e29,e30,e31,e32,e33,e34,e35,e36
,e37,e38,e39,e40,e41,e42,e43,e44,e45,e46,e47,e48,e49,e50,e51,e52,e53
,e54,e55,e56,e57,e58,e59,e60,e61,e62,e63,e64,e65,e66,e67,e68,e69,e70
,e71,e72,e73,e74,e75,e76,e77,e78,e79,e80,e81,e82,e83,e84,e85,e86,e87
,e88,e89,e90,e91,e92,e93,e94,e95,e96,e97,e98,e99,e100,e101,e102,e103
,e104,e105,e106,e107,e108,e109,e110,e111,e112,e113,e114,e115,e116
,e117,e118,e119,e120,e121,e122,e123,e124,e125,e126,e127,e128,e129
,e130,e131,e132,e133,e134,e135,e136,e137,e138,e139,e140,e141,e142
,e143,e144,e145,e146,e147,e148,e149,e150,e151,e152,e153,e154,e155
,e156,e157,e158,e159,e160,e161,e162,e163,e164,e165,e166,e167,e168
,e169,e170,e171,e172,e173,e174,e175,e176,e177,e178,e179,e180,e181
,e182,e183,e184,e185,e186,e187,e188,e189,e190,e191,e192,e193,e194
,e195,e196,e197,e198,e199,e200,e201,e202,e203,e204,e205,e206,e207
,e208,e209;
e1.. x69 + x70 + x71 + x72 + x73 + x74 + x75 + x76 + x77 + x78 + x79 + x80
+ x81 + x82 + x83 - objvar =E= 0;
e2.. (-1.01*x1*x31) - 1.01*x2*x32 - 1.01*x31*x1 - 1.01*x32*x2 + x148 =E= 0;
e3.. (-2.00666666666667*x3*x33) - 2.00666666666667*x4*x34 - 2.00666666666667*
x33*x3 - 2.00666666666667*x34*x4 + x149 =E= 0;
e4.. (-2.38*x5*x35) - 2.38*x6*x36 - 2.38*x35*x5 - 2.38*x36*x6 + x150 =E= 0;
e5.. (-x61*x38*x8) - x61*x37*x7 + x151 =E= 0;
e6.. (-x62*x40*x10) - x62*x39*x9 + x152 =E= 0;
e7.. (-x63*x42*x12) - x63*x41*x11 + x153 =E= 0;
e8.. (-3.29666666666667*x13*x43) - 3.29666666666667*x14*x44 - 3.29666666666667*
x43*x13 - 3.29666666666667*x44*x14 + x154 =E= 0;
e9.. (-x64*x46*x16) - x64*x45*x15 + x155 =E= 0;
e10.. (-x65*x48*x18) - x65*x47*x17 + x156 =E= 0;
e11.. (-x66*x50*x20) - x66*x49*x19 + x157 =E= 0;
e12.. (-x67*x52*x22) - x67*x51*x21 + x158 =E= 0;
e13.. (-40.4533333333333*x23*x53) - 40.4533333333333*x24*x54 - 40.4533333333333
*x53*x23 - 40.4533333333333*x54*x24 + x159 =E= 0;
e14.. (-13.0733333333333*x25*x55) - 13.0733333333333*x26*x56 - 13.0733333333333
*x55*x25 - 13.0733333333333*x56*x26 + x160 =E= 0;
e15.. (-19*x27*x57) - 19*x28*x58 - 19*x57*x27 - 19*x58*x28 + x161 =E= 0;
e16.. (-x68*x60*x30) - x68*x59*x29 + x162 =E= 0;
e17.. x1 + x2 =E= 1;
e18.. x3 + x4 =E= 1;
e19.. x5 + x6 =E= 1;
e20.. x7 + x8 =E= 1;
e21.. x9 + x10 =E= 1;
e22.. x11 + x12 =E= 1;
e23.. x13 + x14 =E= 1;
e24.. x15 + x16 =E= 1;
e25.. x17 + x18 =E= 1;
e26.. x19 + x20 =E= 1;
e27.. x21 + x22 =E= 1;
e28.. x23 + x24 =E= 1;
e29.. x25 + x26 =E= 1;
e30.. x27 + x28 =E= 1;
e31.. x29 + x30 =E= 1;
e32.. 2.02*x1 + 4.01333333333333*x3 + 4.76*x5 + 5.96*x7
+ 42.0933333333333*x9 + 99.28*x11 + 6.59333333333333*x13
+ 61.8666666666667*x15 + 56.2866666666667*x17 + 41.5*x19
+ 62.4933333333333*x21 + 80.9066666666667*x23 + 26.1466666666667*x25
+ 38*x27 + 62.24*x29 =L= 302.08;
e33.. 2.02*x2 + 4.01333333333333*x4 + 4.76*x6 + 5.96*x8
+ 42.0933333333333*x10 + 99.28*x12 + 6.59333333333333*x14
+ 61.8666666666667*x16 + 56.2866666666667*x18 + 41.5*x20
+ 62.4933333333333*x22 + 80.9066666666667*x24 + 26.1466666666667*x26
+ 38*x28 + 62.24*x30 =L= 302.08;
e34.. x84 + x88 =G= 0.29424122;
e35.. x85 + x89 =G= 0.29424122;
e36.. x84 + x90 =G= 0.29760193;
e37.. x85 + x91 =G= 0.29760193;
e38.. x84 + x92 =G= 0.35149534;
e39.. x85 + x93 =G= 0.35149534;
e40.. x84 + x94 =G= 0.30458283;
e41.. x85 + x95 =G= 0.30458283;
e42.. x84 + x96 =G= 0.29951066;
e43.. x85 + x97 =G= 0.29951066;
e44.. x84 + x98 =G= 0.30694357;
e45.. x85 + x99 =G= 0.30694357;
e46.. x84 + x100 =G= 0.33520661;
e47.. x85 + x101 =G= 0.33520661;
e48.. x84 + x102 =G= 0.3400071;
e49.. x85 + x103 =G= 0.3400071;
e50.. x84 + x104 =G= 0.35227087;
e51.. x85 + x105 =G= 0.35227087;
e52.. x84 + x106 =G= 0.34225726;
e53.. x85 + x107 =G= 0.34225726;
e54.. x84 + x108 =G= 0.32776566;
e55.. x85 + x109 =G= 0.32776566;
e56.. x84 + x110 =G= 0.30438256;
e57.. x85 + x111 =G= 0.30438256;
e58.. x84 + x112 =G= 0.28538336;
e59.. x85 + x113 =G= 0.28538336;
e60.. x84 + x114 =G= 0.27950575;
e61.. x85 + x115 =G= 0.27950575;
e62.. - x84 + x88 =G= -0.29424122;
e63.. - x85 + x89 =G= -0.29424122;
e64.. - x84 + x90 =G= -0.29760193;
e65.. - x85 + x91 =G= -0.29760193;
e66.. - x84 + x92 =G= -0.35149534;
e67.. - x85 + x93 =G= -0.35149534;
e68.. - x84 + x94 =G= -0.30458283;
e69.. - x85 + x95 =G= -0.30458283;
e70.. - x84 + x96 =G= -0.29951066;
e71.. - x85 + x97 =G= -0.29951066;
e72.. - x84 + x98 =G= -0.30694357;
e73.. - x85 + x99 =G= -0.30694357;
e74.. - x84 + x100 =G= -0.33520661;
e75.. - x85 + x101 =G= -0.33520661;
e76.. - x84 + x102 =G= -0.3400071;
e77.. - x85 + x103 =G= -0.3400071;
e78.. - x84 + x106 =G= -0.34225726;
e79.. - x85 + x107 =G= -0.34225726;
e80.. - x84 + x108 =G= -0.32776566;
e81.. - x85 + x109 =G= -0.32776566;
e82.. - x84 + x110 =G= -0.30438256;
e83.. - x85 + x111 =G= -0.30438256;
e84.. - x84 + x112 =G= -0.28538336;
e85.. - x85 + x113 =G= -0.28538336;
e86.. - x84 + x114 =G= -0.27950575;
e87.. - x85 + x115 =G= -0.27950575;
e88.. - x84 + x116 =G= -0.25788969;
e89.. - x85 + x117 =G= -0.25788969;
e90.. x86 + x120 =G= -0.9536939;
e91.. x87 + x121 =G= -0.9536939;
e92.. x86 + x122 =G= -0.9004898;
e93.. x87 + x123 =G= -0.9004898;
e94.. x86 + x124 =G= -0.9114032;
e95.. x87 + x125 =G= -0.9114032;
e96.. x86 + x126 =G= -0.90071532;
e97.. x87 + x127 =G= -0.90071532;
e98.. x86 + x128 =G= -0.88043054;
e99.. x87 + x129 =G= -0.88043054;
e100.. x86 + x130 =G= -0.8680249;
e101.. x87 + x131 =G= -0.8680249;
e102.. x86 + x132 =G= -0.81034814;
e103.. x87 + x133 =G= -0.81034814;
e104.. x86 + x134 =G= -0.80843127;
e105.. x87 + x135 =G= -0.80843127;
e106.. x86 + x136 =G= -0.7794471;
e107.. x87 + x137 =G= -0.7794471;
e108.. x86 + x138 =G= -0.79930922;
e109.. x87 + x139 =G= -0.79930922;
e110.. x86 + x140 =G= -0.84280733;
e111.. x87 + x141 =G= -0.84280733;
e112.. x86 + x142 =G= -0.81379236;
e113.. x87 + x143 =G= -0.81379236;
e114.. x86 + x144 =G= -0.82457178;
e115.. x87 + x145 =G= -0.82457178;
e116.. x86 + x146 =G= -0.80226439;
e117.. x87 + x147 =G= -0.80226439;
e118.. - x86 + x118 =G= 0.98493628;
e119.. - x87 + x119 =G= 0.98493628;
e120.. - x86 + x120 =G= 0.9536939;
e121.. - x87 + x121 =G= 0.9536939;
e122.. - x86 + x122 =G= 0.9004898;
e123.. - x87 + x123 =G= 0.9004898;
e124.. - x86 + x124 =G= 0.9114032;
e125.. - x87 + x125 =G= 0.9114032;
e126.. - x86 + x126 =G= 0.90071532;
e127.. - x87 + x127 =G= 0.90071532;
e128.. - x86 + x128 =G= 0.88043054;
e129.. - x87 + x129 =G= 0.88043054;
e130.. - x86 + x130 =G= 0.8680249;
e131.. - x87 + x131 =G= 0.8680249;
e132.. - x86 + x132 =G= 0.81034814;
e133.. - x87 + x133 =G= 0.81034814;
e134.. - x86 + x134 =G= 0.80843127;
e135.. - x87 + x135 =G= 0.80843127;
e136.. - x86 + x138 =G= 0.79930922;
e137.. - x87 + x139 =G= 0.79930922;
e138.. - x86 + x140 =G= 0.84280733;
e139.. - x87 + x141 =G= 0.84280733;
e140.. - x86 + x142 =G= 0.81379236;
e141.. - x87 + x143 =G= 0.81379236;
e142.. - x86 + x144 =G= 0.82457178;
e143.. - x87 + x145 =G= 0.82457178;
e144.. - x86 + x146 =G= 0.80226439;
e145.. - x87 + x147 =G= 0.80226439;
e146.. x31 - x88 - x118 =E= 0;
e147.. x32 - x89 - x119 =E= 0;
e148.. x33 - x90 - x120 =E= 0;
e149.. x34 - x91 - x121 =E= 0;
e150.. x35 - x92 - x122 =E= 0;
e151.. x36 - x93 - x123 =E= 0;
e152.. x37 - x94 - x124 =E= 0;
e153.. x38 - x95 - x125 =E= 0;
e154.. x39 - x96 - x126 =E= 0;
e155.. x40 - x97 - x127 =E= 0;
e156.. x41 - x98 - x128 =E= 0;
e157.. x42 - x99 - x129 =E= 0;
e158.. x43 - x100 - x130 =E= 0;
e159.. x44 - x101 - x131 =E= 0;
e160.. x45 - x102 - x132 =E= 0;
e161.. x46 - x103 - x133 =E= 0;
e162.. x47 - x104 - x134 =E= 0;
e163.. x48 - x105 - x135 =E= 0;
e164.. x49 - x106 - x136 =E= 0;
e165.. x50 - x107 - x137 =E= 0;
e166.. x51 - x108 - x138 =E= 0;
e167.. x52 - x109 - x139 =E= 0;
e168.. x53 - x110 - x140 =E= 0;
e169.. x54 - x111 - x141 =E= 0;
e170.. x55 - x112 - x142 =E= 0;
e171.. x56 - x113 - x143 =E= 0;
e172.. x57 - x114 - x144 =E= 0;
e173.. x58 - x115 - x145 =E= 0;
e174.. x59 - x116 - x146 =E= 0;
e175.. x60 - x117 - x147 =E= 0;
e176.. b164 + b165 =G= 1;
e177.. b163 + b165 =G= 1;
e178.. b163 + b164 =G= 1;
e179.. b165 + b167 =G= 1;
e180.. b165 + b166 =G= 1;
e181.. b164 + b167 =G= 1;
e182.. b164 + b166 =G= 1;
e183.. b163 + b167 =G= 1;
e184.. b163 + b166 =G= 1;
e185.. b168 - b169 =G= 0;
e186.. x86 - x87 =G= 0;
e187.. x61 - 0.28*b163 =E= 5.68;
e188.. x62 - 1.91333333333333*b164 =E= 40.18;
e189.. x63 - 4.51333333333333*b165 =E= 94.7666666666667;
e190.. x64 - 2.81333333333333*b166 =E= 59.0533333333333;
e191.. x65 - 2.55333333333333*b167 =E= 53.7333333333333;
e192.. x66 - 1.88666666666667*b168 - 1.88666666666667*b169
=E= 37.7266666666667;
e193.. x67 - 2.84666666666667*b170 =E= 59.6466666666667;
e194.. x68 - 2.96666666666667*b171 =E= 59.2733333333333;
e195.. - x69 + x148 =L= 0;
e196.. - x70 + x149 =L= 0;
e197.. - x71 + x150 =L= 0;
e198.. - x72 + x151 =L= 0;
e199.. - x73 + x152 =L= 0;
e200.. - x74 + x153 =L= 0;
e201.. - x75 + x154 =L= 0;
e202.. - x76 + x155 =L= 0;
e203.. - x77 + x156 =L= 0;
e204.. - x78 + x157 =L= 0;
e205.. - x79 + x158 =L= 0;
e206.. - x80 + x159 =L= 0;
e207.. - x81 + x160 =L= 0;
e208.. - x82 + x161 =L= 0;
e209.. - x83 + x162 =L= 0;
* set non-default bounds
x1.up = 1;
x2.up = 1;
x3.up = 1;
x4.up = 1;
x5.up = 1;
x6.up = 1;
x7.up = 1;
x8.up = 1;
x9.up = 1;
x10.up = 1;
x11.up = 1;
x12.up = 1;
x13.up = 1;
x14.up = 1;
x15.up = 1;
x16.up = 1;
x17.up = 1;
x18.up = 1;
x19.up = 1;
x20.up = 1;
x21.up = 1;
x22.up = 1;
x23.up = 1;
x24.up = 1;
x25.up = 1;
x26.up = 1;
x27.up = 1;
x28.up = 1;
x29.up = 1;
x30.up = 1;
x31.up = 0.26351883;
x32.up = 0.26351883;
x33.up = 0.22891574;
x34.up = 0.22891574;
x35.up = 0.21464835;
x36.up = 0.21464835;
x37.up = 0.17964414;
x38.up = 0.17964414;
x39.up = 0.17402843;
x40.up = 0.17402843;
x41.up = 0.15355962;
x42.up = 0.15355962;
x43.up = 0.1942283;
x44.up = 0.1942283;
x45.up = 0.25670555;
x46.up = 0.25670555;
x47.up = 0.27088619;
x48.up = 0.27088619;
x49.up = 0.28985675;
x50.up = 0.28985675;
x51.up = 0.25550303;
x52.up = 0.25550303;
x53.up = 0.19001726;
x54.up = 0.19001726;
x55.up = 0.23803143;
x56.up = 0.23803143;
x57.up = 0.23312962;
x58.up = 0.23312962;
x59.up = 0.27705307;
x60.up = 0.27705307;
x61.up = 5.96;
x62.up = 42.0933333333333;
x63.up = 99.28;
x64.up = 61.8666666666667;
x65.up = 56.2866666666667;
x66.up = 41.5;
x67.up = 62.4933333333333;
x68.up = 62.24;
x69.up = 0.5323080366;
x70.up = 0.918715169866666;
x71.up = 1.021726146;
x72.up = 1.0706790744;
x73.up = 7.32543671346667;
x74.up = 15.2453990736;
x75.up = 1.28061192466667;
x76.up = 15.8815166933333;
x77.up = 15.2472806811333;
x78.up = 12.029055125;
x79.up = 15.9672360214667;
x80.up = 15.3736631157333;
x81.up = 6.2237284564;
x82.up = 8.85892556;
x83.up = 17.2437830768;
x84.lo = 0.25788969; x84.up = 0.35227087;
x85.lo = 0.25788969; x85.up = 0.35227087;
x86.lo = -0.98493628; x86.up = -0.7794471;
x87.lo = -0.98493628; x87.up = -0.7794471;
x88.up = 0.0580296499999999;
x89.up = 0.0580296499999999;
x90.up = 0.0546689399999999;
x91.up = 0.0546689399999999;
x92.up = 0.09360565;
x93.up = 0.09360565;
x94.up = 0.0476880399999999;
x95.up = 0.0476880399999999;
x96.up = 0.05276021;
x97.up = 0.05276021;
x98.up = 0.04905388;
x99.up = 0.04905388;
x100.up = 0.07731692;
x101.up = 0.07731692;
x102.up = 0.08211741;
x103.up = 0.08211741;
x104.up = 0.09438118;
x105.up = 0.09438118;
x106.up = 0.08436757;
x107.up = 0.08436757;
x108.up = 0.06987597;
x109.up = 0.06987597;
x110.up = 0.04788831;
x111.up = 0.04788831;
x112.up = 0.0668875099999999;
x113.up = 0.0668875099999999;
x114.up = 0.07276512;
x115.up = 0.07276512;
x116.up = 0.09438118;
x117.up = 0.09438118;
x118.up = 0.20548918;
x119.up = 0.20548918;
x120.up = 0.1742468;
x121.up = 0.1742468;
x122.up = 0.1210427;
x123.up = 0.1210427;
x124.up = 0.1319561;
x125.up = 0.1319561;
x126.up = 0.12126822;
x127.up = 0.12126822;
x128.up = 0.10450574;
x129.up = 0.10450574;
x130.up = 0.11691138;
x131.up = 0.11691138;
x132.up = 0.17458814;
x133.up = 0.17458814;
x134.up = 0.17650501;
x135.up = 0.17650501;
x136.up = 0.20548918;
x137.up = 0.20548918;
x138.up = 0.18562706;
x139.up = 0.18562706;
x140.up = 0.14212895;
x141.up = 0.14212895;
x142.up = 0.17114392;
x143.up = 0.17114392;
x144.up = 0.1603645;
x145.up = 0.1603645;
x146.up = 0.18267189;
x147.up = 0.18267189;
x148.up = 0.5323080366;
x149.up = 0.918715169866666;
x150.up = 1.021726146;
x151.up = 1.0706790744;
x152.up = 7.32543671346667;
x153.up = 15.2453990736;
x154.up = 1.28061192466667;
x155.up = 15.8815166933333;
x156.up = 15.2472806811333;
x157.up = 12.029055125;
x158.up = 15.9672360214667;
x159.up = 15.3736631157333;
x160.up = 6.2237284564;
x161.up = 8.85892556;
x162.up = 17.2437830768;
Model m / all /;
m.limrow=0; m.limcol=0;
m.tolproj=0.0;
$if NOT '%gams.u1%' == '' $include '%gams.u1%'
$if not set MINLP $set MINLP MINLP
Solve m using %MINLP% minimizing objvar;
Last updated: 2025-08-07 Git hash: e62cedfc