MINLPLib

A Library of Mixed-Integer and Continuous Nonlinear Programming Instances

Home // Instances // Documentation // Download // Statistics

Instance shiporig

This model designs a vertically corrugated transverse bulkhead of an oil tanker.
The objective is to design for minimum weight and meet stress, moment of inertia and plate thickness constraints.
This version of ship corresponds to the current version of ship from the GAMS model library.
It corresponds to the original version from the paper, plus an extra lower bound on variable x10.

Formatsⓘ	ams gms mod nl osil py
Primal Bounds (infeas ≤ 1e-08)ⓘ	5.54091471 p1 ( gdx sol ) (infeas: 4e-12)
Other points (infeas > 1e-08)ⓘ
Dual Boundsⓘ	0.00000000 (ANTIGONE) 0.00000000 (BARON) 0.00000000 (COUENNE) 5.54091471 (LINDO) -99999999809999994880.00000000 (SCIP)
Referencesⓘ	Bracken, Jerome and McCormick, Garth P, Chapter 6. In Bracken, Jerome and McCormick, Garth P, Selected Applications of Nonlinear Programming, John Wiley and Sons, New York, 1968.
Sourceⓘ	GAMS Model Library model ship
Applicationⓘ	Structural Optimization
Added to libraryⓘ	15 Aug 2014
Problem typeⓘ	NLP
#Variablesⓘ	10
#Binary Variablesⓘ	0
#Integer Variablesⓘ	0
#Nonlinear Variablesⓘ	10
#Nonlinear Binary Variablesⓘ	0
#Nonlinear Integer Variablesⓘ	0
Objective Senseⓘ	min
Objective typeⓘ	signomial
Objective curvatureⓘ	indefinite
#Nonzeros in Objectiveⓘ	6
#Nonlinear Nonzeros in Objectiveⓘ	6
#Constraintsⓘ	17
#Linear Constraintsⓘ	10
#Quadratic Constraintsⓘ	0
#Polynomial Constraintsⓘ	3
#Signomial Constraintsⓘ	3
#General Nonlinear Constraintsⓘ	1
Operands in Gen. Nonlin. Functionsⓘ	mul sqrt
Constraints curvatureⓘ	indefinite
#Nonzeros in Jacobianⓘ	48
#Nonlinear Nonzeros in Jacobianⓘ	23
#Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ	41
#Nonzeros in Diagonal of Hessian of Lagrangianⓘ	3
#Blocks in Hessian of Lagrangianⓘ	1
Minimal blocksize in Hessian of Lagrangianⓘ	10
Maximal blocksize in Hessian of Lagrangianⓘ	10
Average blocksize in Hessian of Lagrangianⓘ	10.0
#Semicontinuitiesⓘ	0
#Nonlinear Semicontinuitiesⓘ	0
#SOS type 1ⓘ	0
#SOS type 2ⓘ	0
Minimal coefficientⓘ	3.9000e-03
Maximal coefficientⓘ	4.9500e+02
Infeasibility of initial pointⓘ	407.3
Sparsity Jacobianⓘ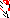
Sparsity Hessian of Lagrangianⓘ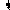

$offlisting
*  
*  Equation counts
*      Total        E        G        L        N        X        C        B
*         18        5       13        0        0        0        0        0
*  
*  Variable counts
*                   x        b        i      s1s      s2s       sc       si
*      Total     cont   binary  integer     sos1     sos2    scont     sint
*         11       11        0        0        0        0        0        0
*  FX      0
*  
*  Nonzero counts
*      Total    const       NL      DLL
*         55       26       29        0
*
*  Solve m using NLP minimizing objvar;


Variables  x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,objvar;

Equations  e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13,e14,e15,e16,e17,e18;


e1.. -0.5*x9*x4*(0.8*x7 + 0.333333333333333*x8) + x1 =E= 0;

e2.. -0.5*x9*x5*(0.8*x7 + 0.333333333333333*x8) + x2 =E= 0;

e3.. -0.5*x9*x6*(0.8*x7 + 0.333333333333333*x8) + x3 =E= 0;

e4.. -sqrt(x8*x8 - x9*x9) - x7 + x10 =E= 0;

e5..    x1 - 8.4652734375*x10 =G= 0;

e6..    x2 - 9.65006510416667*x10 =G= 0;

e7..    x3 - 8.8716796875*x10 =G= 0;

e8.. 0.5*x1*x9 - 2.2*(8.4652734375*x10)**1.33333333333333 =G= 0;

e9.. 0.5*x2*x9 - 2.2*(9.65006510416667*x10)**1.33333333333333 =G= 0;

e10.. 0.5*x3*x9 - 2.2*(8.8716796875*x10)**1.33333333333333 =G= 0;

e11..    x4 - 0.0111771747883801*x7 =G= 0.2;

e12..    x5 - 0.0137655360411427*x7 =G= 0.2;

e13..    x6 - 0.0155663872253648*x7 =G= 0.2;

e14..    x4 - 0.0111771747883801*x8 =G= 0.2;

e15..    x5 - 0.0137655360411427*x8 =G= 0.2;

e16..    x6 - 0.0155663872253648*x8 =G= 0.2;

e17..    x8 - x9 =G= 0;

e18.. -(0.0039*x7 + 0.0039*x8)*(495*x4 + 385*x5 + 315*x6)/x10 + objvar =E= 0;

* set non-default bounds
x4.lo = 1.05;
x5.lo = 1.05;
x6.lo = 1.05;
x10.lo = 1;

* set non-default levels
x1.l = 934.032;
x2.l = 934.032;
x3.l = 1011.868;
x4.l = 1.2;
x5.l = 1.2;
x6.l = 1.3;
x7.l = 45.8;
x8.l = 43.2;
x9.l = 30.5;
x10.l = 76.3939536510076;

Model m / all /;

m.limrow=0; m.limcol=0;
m.tolproj=0.0;

$if NOT '%gams.u1%' == '' $include '%gams.u1%'

$if not set NLP $set NLP NLP
Solve m using %NLP% minimizing objvar;