MINLPLib
A Library of Mixed-Integer and Continuous Nonlinear Programming Instances
Home // Instances // Documentation // Download // Statistics
Instance water
| Formatsⓘ | ams gms mod nl osil py |
| Primal Bounds (infeas ≤ 1e-08)ⓘ | |
| Other points (infeas > 1e-08)ⓘ | |
| Dual Boundsⓘ | 681.81933800 (BARON) 324.68461220 (COUENNE) 670.36320240 (LINDO) 826.50997960 (SCIP) |
| Referencesⓘ | Brooke, Anthony, Drud, Arne S, and Meeraus, Alexander, Modeling Systems and Nonlinear Programming in a Research Environment. In Ragavan, R and Rohde, S M, Eds, Computers in Engineering, Vol. III, ACME, 1985. Drud, Arne S and Rosenborg, A, Dimensioning Water Distribution Networks, Masters thesis, Institute of Mathematical Statistics and Operations Research, Technical University of Denmark, 1973. In Danish. |
| Sourceⓘ | GAMS Model Library model water |
| Applicationⓘ | Water Network Design |
| Added to libraryⓘ | 31 Jul 2001 |
| Problem typeⓘ | NLP |
| #Variablesⓘ | 41 |
| #Binary Variablesⓘ | 0 |
| #Integer Variablesⓘ | 0 |
| #Nonlinear Variablesⓘ | 32 |
| #Nonlinear Binary Variablesⓘ | 0 |
| #Nonlinear Integer Variablesⓘ | 0 |
| Objective Senseⓘ | min |
| Objective typeⓘ | linear |
| Objective curvatureⓘ | linear |
| #Nonzeros in Objectiveⓘ | 3 |
| #Nonlinear Nonzeros in Objectiveⓘ | 0 |
| #Constraintsⓘ | 25 |
| #Linear Constraintsⓘ | 9 |
| #Quadratic Constraintsⓘ | 1 |
| #Polynomial Constraintsⓘ | 0 |
| #Signomial Constraintsⓘ | 1 |
| #General Nonlinear Constraintsⓘ | 14 |
| Operands in Gen. Nonlin. Functionsⓘ | abs div mul vcpower |
| Constraints curvatureⓘ | indefinite |
| #Nonzeros in Jacobianⓘ | 109 |
| #Nonlinear Nonzeros in Jacobianⓘ | 46 |
| #Nonzeros in (Upper-Left) Hessian of Lagrangianⓘ | 60 |
| #Nonzeros in Diagonal of Hessian of Lagrangianⓘ | 28 |
| #Blocks in Hessian of Lagrangianⓘ | 16 |
| Minimal blocksize in Hessian of Lagrangianⓘ | 2 |
| Maximal blocksize in Hessian of Lagrangianⓘ | 2 |
| Average blocksize in Hessian of Lagrangianⓘ | 2.0 |
| #Semicontinuitiesⓘ | 0 |
| #Nonlinear Semicontinuitiesⓘ | 0 |
| #SOS type 1ⓘ | 0 |
| #SOS type 2ⓘ | 0 |
| Minimal coefficientⓘ | 6.9000e-02 |
| Maximal coefficientⓘ | 2.5020e+03 |
| Infeasibility of initial pointⓘ | 723.6 |
| Sparsity Jacobianⓘ | 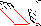 |
| Sparsity Hessian of Lagrangianⓘ | 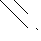 |
$offlisting
*
* Equation counts
* Total E G L N X C B
* 26 26 0 0 0 0 0 0
*
* Variable counts
* x b i s1s s2s sc si
* Total cont binary integer sos1 sos2 scont sint
* 42 42 0 0 0 0 0 0
* FX 0
*
* Nonzero counts
* Total const NL DLL
* 113 67 46 0
*
* Solve m using DNLP minimizing objvar;
Variables x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19
,x20,x21,x22,x23,x24,x25,x26,x27,x28,x29,x30,x31,x32,x33,x34,x35,x36
,x37,x38,x39,x40,x41,objvar;
Positive Variables x37,x38;
Equations e1,e2,e3,e4,e5,e6,e7,e8,e9,e10,e11,e12,e13,e14,e15,e16,e17,e18,e19
,e20,e21,e22,e23,e24,e25,e26;
e1.. - x1 - x2 - x3 + x37 =E= 0;
e2.. - x4 - x5 - x6 - x7 + x38 =E= 0;
e3.. x1 + x4 - x8 - x9 - x10 - x11 =E= 1.212;
e4.. x2 + x8 + x12 =E= 0.452;
e5.. x9 - x12 + x13 =E= 0.245;
e6.. x5 + x10 - x13 - x14 =E= 0.652;
e7.. x6 + x14 =E= 0.252;
e8.. x3 + x7 + x11 =E= 0.456;
e9.. -1.5722267648148*abs(x1)*x1/x15**5.33 + x29 - x31 =E= 0;
e10.. -1.32004857865156*abs(x2)*x2/x16**5.33 + x29 - x32 =E= 0;
e11.. -2.57705917665854*abs(x3)*x3/x17**5.33 + x29 - x36 =E= 0;
e12.. -2.06257339263358*abs(x4)*x4/x18**5.33 + x30 - x31 =E= 0;
e13.. -2.40235218067626*abs(x5)*x5/x19**5.33 + x30 - x34 =E= 0;
e14.. -1.339*abs(x6)*x6/x20**5.33 + x30 - x35 =E= 0;
e15.. -1.37419139860501*abs(x7)*x7/x21**5.33 + x30 - x36 =E= 0;
e16.. -1.2916134290104*abs(x8)*x8/x22**5.33 + x31 - x32 =E= 0;
e17.. -1.60230396616872*abs(x9)*x9/x23**5.33 + x31 - x33 =E= 0;
e18.. -1.339*abs(x10)*x10/x24**5.33 + x31 - x34 =E= 0;
e19.. -2.14329116080854*abs(x11)*x11/x25**5.33 + x31 - x36 =E= 0;
e20.. -1.24561882211213*abs(x12)*x12/x26**5.33 - x32 + x33 =E= 0;
e21.. -1.15157500841239*abs(x13)*x13/x27**5.33 - x33 + x34 =E= 0;
e22.. -2.06257339263358*abs(x14)*x14/x28**5.33 + x34 - x35 =E= 0;
e23.. -(1.02*x37*(-6.5 + x29) + 1.02*x38*(-3.25 + x30)) + x39 =E= 0;
e24.. -0.069*(1526.43375224737*x15**1.29 + 1281.60056179763*x16**1.29 +
2501.99920063936*x17**1.29 + 2002.49843945008*x18**1.29 +
2332.38075793812*x19**1.29 + 1300*x20**1.29 + 1334.16640641263*x21**1.29
+ 1253.99362039845*x22**1.29 + 1555.6349186104*x23**1.29 + 1300*x24**
1.29 + 2080.86520466848*x25**1.29 + 1209.33866224478*x26**1.29 +
1118.03398874989*x27**1.29 + 2002.49843945008*x28**1.29) + x40 =E= 0;
e25.. - 0.2*x37 - 0.17*x38 + x41 =E= 0;
e26.. - 10*x39 - x40 - 10*x41 + objvar =E= 0;
* set non-default bounds
x15.lo = 0.15; x15.up = 2;
x16.lo = 0.15; x16.up = 2;
x17.lo = 0.15; x17.up = 2;
x18.lo = 0.15; x18.up = 2;
x19.lo = 0.15; x19.up = 2;
x20.lo = 0.15; x20.up = 2;
x21.lo = 0.15; x21.up = 2;
x22.lo = 0.15; x22.up = 2;
x23.lo = 0.15; x23.up = 2;
x24.lo = 0.15; x24.up = 2;
x25.lo = 0.15; x25.up = 2;
x26.lo = 0.15; x26.up = 2;
x27.lo = 0.15; x27.up = 2;
x28.lo = 0.15; x28.up = 2;
x29.lo = 6.5;
x30.lo = 3.25;
x31.lo = 16.58;
x32.lo = 14.92;
x33.lo = 12.925;
x34.lo = 12.26;
x35.lo = 8.76;
x36.lo = 16.08;
x37.up = 2.5;
x38.up = 6;
* set non-default levels
x15.l = 0.547722557505166;
x16.l = 0.547722557505166;
x17.l = 0.547722557505166;
x18.l = 0.547722557505166;
x19.l = 0.547722557505166;
x20.l = 0.547722557505166;
x21.l = 0.547722557505166;
x22.l = 0.547722557505166;
x23.l = 0.547722557505166;
x24.l = 0.547722557505166;
x25.l = 0.547722557505166;
x26.l = 0.547722557505166;
x27.l = 0.547722557505166;
x28.l = 0.547722557505166;
x29.l = 7.5;
x30.l = 4.25;
x31.l = 17.58;
x32.l = 15.92;
x33.l = 13.925;
x34.l = 13.26;
x35.l = 9.76;
x36.l = 17.08;
x37.l = 0.961470588235294;
x38.l = 2.30752941176471;
Model m / all /;
m.limrow=0; m.limcol=0;
m.tolproj=0.0;
$if NOT '%gams.u1%' == '' $include '%gams.u1%'
$if not set DNLP $set DNLP DNLP
Solve m using %DNLP% minimizing objvar;
Last updated: 2025-08-07 Git hash: e62cedfc